第５６問の解答

---

１．問題　［平面図形］

左図のような、ドーナッツ型の板を右方向に２０ｃｍだけ転がしたとき、板が通過する部分の面積は何ｃｍ2でしょうか？ ただし、大きい方の円の半径は２０ｃｍ、小さい方の円の面積は大きい方の円の面積のちょうど半分です。 また、円周率π＝３．１４として計算して下さい。

---

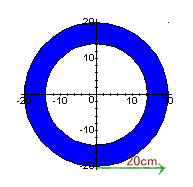２．解答例1（かめちゃさん、わかさひ君、ありさのお父さん他）

ドーナッツ型の板を２０ｃｍ転がすと下図のようになります。

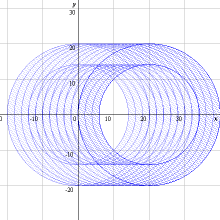
そこで、下図のように最初と最後の円の中心をＯ、Ｐとし、Ｏ、Ｐを通る垂直な直径をＡＢ、ＤＣ、そして正方形ＡＯＰＤの対角線の交点をＥ、正方形ＯＢＣＰの対角線の交点をＦとします。

　

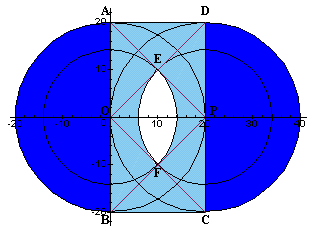
　まず、大小２つの円の半径をＲ、ｒとします。題意より、π×Ｒ²：π×ｒ²＝２：１。
よって、Ｒ²：ｒ²＝２：１。

直角２等辺三角形ＡＯＰの面積＝正方形ＡＯＰＤの面積×１／２＝ＯＥ^２。
従って、Ｒ²：ＯＥ^２＝２：１。

これより、ＯＥ＝ｒとなり、Ｅ、Ｆが最初の小さい円の円周上にあることを示す。
全く同様にして、Ｅ、Ｆが最後の小さい円の円周上にもあることとなるので、結局上図の白いレンズの部分の端点であることが分かる。

また、∠ＥＯＦ＝∠ＥＯＰ＋∠ＦＯＰ＝９０度。

さて、求める面積をＳ0、レンズ部分の面積をＳ1とすると、
Ｓ0＋Ｓ1＝大きい円の半分＋正方形ＡＯＰＤの面積×２＋大きい円の半分
　　　　　 ＝π×Ｒ²／２＋Ｒ²×２＋π×Ｒ²／２
　　　　　＝（π＋２）×Ｒ²。

また、
Ｓ1／２＝扇形ＯＥＦの面積−直角三角形ＯＥＦの面積
　　　　＝π×ｒ²／４−ｒ²／２
　　　　＝（π／４−１／２）×ｒ²
　　　　＝（π／４−１／２）×Ｒ²／２。

従って、Ｓ0＝（π＋２）×Ｒ²−（π／４−１／２）×Ｒ²
　　　　　　 ＝（π×３／４＋５／２）×Ｒ²
　　　　　　　＝（３．１４×３／４＋５／２）×２０²
　　　　　　　＝１９４２ｃｍ²。

答：１９４２ｃｍ²

以上

---