第５７問の解答

---

１．問題　［場合の数・数列］

左図のような、正四面体の頂点Ａに今います。 １秒後には、他の３つの頂点のどれかに移動します。 移動のしかたには、特に制限はありません。例えば次の１秒後に再び元の頂点Ａに戻ってもかまいません。ただし、同じ場所に止まってはいけません。 このように移動を続けて、７秒後に頂点Ａにいるような動き方は何通りあるでしょう？

---

２．解答例1（長野　美光さん、ｋｕｒｉ他）

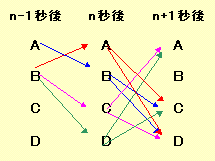
移動できる状況を図で表すと下図のようになります。

そこで、ｎ秒後に頂点Ａ、頂点Ｂ、頂点Ｃ、頂点Ｄに移動できる場合の数をａ_n、ｂ_n、ｃ_n、ｄ_nとします。
すると上図から、
　　ａ_n+1＝ｂ_n＋ｃ_n＋ｄ_n　・・・　（１）
　　ｂ_n+1＝ａ_n＋ｃ_n＋ｄ_n　・・・　（２）
　　ｃ_n+1＝ａ_n＋ｂ_n＋ｄ_n　・・・　（３）
　　ｄ_n+1＝ａ_n＋ｂ_n＋ｃ_n　・・・　（４）
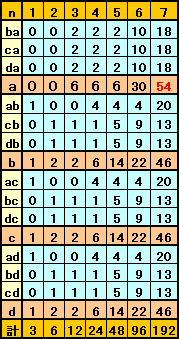
と表せます。ただし、初期値はａ₀=１、ｂ₀=0、ｃ₀=0、ｄ₀=0です。

これらの式に従って、順次計算していくと下表のようａ₇=５４６になります。

　

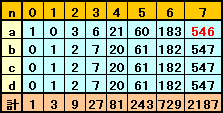
　答：５４６通り

以上

---

３．解答例２（あれふさん、井合宗太郎さん他）

前述の漸化式を加えて、（１）＋（２）＋（３）＋（４）より、
　　ａ_n+1＋ｂ_n+1＋ｃ_n+1＋ｄ_n+1＝（ａ_n＋ｂ_n＋ｃ_n＋ｄ_n）×３
となるので、ａ_n＋ｂ_n＋ｃ_n＋ｄ_nは、初項ａ₀＋ｂ₀＋ｃ₀＋ｄ₀＝１で公比が３の等比数列となります。従って、ａ_n＋ｂ_n＋ｃ_n＋ｄ_n＝３ⁿとなります。

従って、
　　ａ_n+1＋ａ_n＝（ｂ_n＋ｃ_n＋ｄ_n）＋ａ_n＝３ⁿ　・・・　（５）
　　ａ_n+1＝３ⁿ−ａ_n　　　　　　　　　　　　　　　・・・　（６）
が得られます。

（６）を用いて、順次計算して、下表のようにａ₇=５４６が求まります。

---

４．解答例３（Ｂ２さん他）

（５）式を用いて、ａ_nの一般式を求めましょう。

（補題）次のような漸化式（線型漸化式といいます） 　　ａn+m＋pm-1ａn+m-1＋pm-2ａn+m-2・・・＋p0ａn=0 　に対して、 　　xm＋pmxm-1＋pm-1xm-2・・・＋p1=0 　の解をα1、α2、・・・αmとします（重根はないものとします）。 　このとき、 　　ａn＝Ａ1α1n-1＋Ａ2α2n-1＋・・・＋Ａmαmn-1 　と表すことが出来ます。

　

（方法１）
　　（５）より、
　　　ａ_n+1−1/4×３ⁿ⁺¹＝−（ａ_n−1/4×３ⁿ）
　　を得るので、ａ_n−1/4×３ⁿは、公比−１、初項ａ₀−1/4×３⁰＝3/4なる等比数列。
　　よって、ａ_n−1/4×３ⁿ＝3/4×（−１）^ｎとなり、
　　　ａ_n＝1/4×３ⁿ＋3/4×（−１）^ｎ
　　が得られます。

（方法２）
　　（５）より、
　　　ａ_n+2＋ａ_n+1＝３ⁿ⁺¹　・・・　（７）
　　（７）−（５）×３より、
　　　ａ_n+2＋ａ_n+1−（ａ_n+1＋ａ_n）×３＝０
　　よって、ａ_n+2−２×ａ_n+1−３×ａ_n＝０なる線型漸化式を得る。

　　従って補題より、x²−２x−３=0をまず解きます。
　　（x−３）×（x＋１）＝０となり、x＝３、x＝−１が得られます。
　　よって、　ａ_n＝Ａ₁×３ⁿ＋Ａ₂×（−１）ⁿを得ます。
　　ここで、Ａ₁、Ａ₂は、
　　　ａ₀＝Ａ₁＋Ａ₂＝１、ａ₁＝３×Ａ₁−Ａ₂＝０
　　から、Ａ₁＝１／４、Ａ₂＝３／４を得ます。
　　
　従って、ａ_n＝1/4×３ⁿ＋3/4×（−１）^ｎとなります。

（補題の証明１）m=3とします。 　　ａn+3＋p2ａn+2＋p1ａn+1＋p0ａn=0 　に対して、x3＋p3x2＋p2x＋p1=0　の解をα1、α2、α3とします。 　このとき、 　　bn＝Ａ1α1n-1＋Ａ2α2n-1＋Ａ3α3n-1とします。 　ただし、Ａ1、Ａ2、Ａ3は、　 　Ａ1＋Ａ2＋Ａ3＝ａ1、Ａ1α1＋Ａ2α2＋Ａ3α3＝ａ2、Ａ1α12＋Ａ2α22＋Ａ3α32＝ａ3 を解いて求めることとします。 　証明は数学的帰納法を用います。 （１）b1＝ａ1、b2＝ａ2、b3＝ａ3は明らか。 （２）n≦k（ただし、k≧３）のとき、bn＝ａnが成り立つとします。 　　n=k+1のとき、 　　bn＝Ａ1α1k＋Ａ2α2k＋Ａ3α3k 　　　＝Ａ1α1k-3×α13＋Ａ2α2k-3×α23＋Ａ3α3k-3×α33 　　　＝−Ａ1α1k-3×（p3α12＋p2α1＋p1）＋Ａ2α2k-3×（p3α22＋p2α2＋p1） 　　　　　＋Ａ3α3k-3×（p3α32＋p2α3＋p1） 　　　＝−p3×（Ａ1α1k-1＋Ａ2α2k-1＋Ａ3α3k-1）−p2×（Ａ1α1k-2＋Ａ2α2k-2＋Ａ3α3k-2） 　　　　　−p1×（Ａ1α1k-3＋Ａ2α2k-3＋Ａ3α3k-3） 　　　＝−p3×ｂk−p2×ｂk-1−p1×ｂk-2 　　　＝−p3×ａk−p2×ａk-1−p1×ａk-2（仮定より） 　　　＝ａk+1 　よって、n=k+1のときもbn＝ａnが成り立つ。 　以上から、数学的帰納法により、全てのｎについて、bn＝ａnが成り立つ。 （補題の証明2）m=2とします。 ａn+2＋p1ａn+1＋p0ａn=0に対して、x2＋p2x＋p1=0　の解をα1、α2とします。 ２次方程式の根と係数の関係より、α1＋α2＝−p2、α1×α2＝p1となります。 これから、漸化式を次のように変形します。 　　ａn+2−（α1＋α2）ａn+1＋α1α2ａn＝0 　　ａn+2−α1ａn+1−α2（ａn+1−α1ａn）＝0 これは、ａn+1−α1ａnが公比α2となることを表しているので、 　　ａn+1−α1ａn＝Ｃ1α2n-1　・・・（８）　と表せます。ただし、Ｃ1は定数。 まったく同様にして、 　　ａn+1−α2ａn＝Ｃ2α1n-1　・・・（９）　と表せます。 （９）−（８）より、 　　（α1−α2）ａn＝Ｃ2α1n-1−Ｃ1α2n-1 α1とα2は異なるので、 　　ａn＝Ｃ2／（α1−α2）α1n-1−Ｃ1／（α1−α2）α2n-1 　　Ａ1＝Ｃ2／（α1−α2）、Ａ2＝−Ｃ1／（α1−α2）とおけば、 　　ａn＝Ａ1α1n-1＋Ａ2α2n-1　と表せます。 　以上

---

（参考問題：武田 浩紀さんによる）

１秒前と同じ頂点には戻ってはいけないという制限を加えた場合、７秒後に頂点Ａにいるような動き方は何通りあるでしょう？

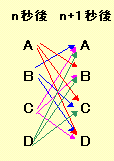
移動できる条件は、下図のように１秒目の状態に影響されます。

そこで、１秒前にはＢにいて現在Ａにいる場合の数をba(n+1)のように表すことにします。
漸化式および初期値は、次の通り。　

ba(n+1)=cb(n)+db(n) ca(n+1)=bc(n)+dc(n) da(n+1)=bd(n)+cd(n)	ab(n+1)=ca(n)+da(n) cb(n+1)=ac(n)+dc(n) db(n+1)=ad(n)+cd(n)	ac(n+1)=ba(n)+da(n) bc(n+1)=ab(n)+db(n) dc(n+1)=ad(n)+bd(n)	ad(n+1)=ba(n)+ca(n) bd(n+1)=ab(n)+cb(n) cd(n+1)=ac(n)+bc(n)
ba(1)=0 ca(1)=0 da(1)=0	ab(1)=1 cb(1)=0 db(1)=0	ac(1)=1 bc(1)=0 dc(1)=0	ad(1)=1 bd(1)=0 cd(1)=0

この漸化式に従って順次計算していけば、下表のようになる。

よって、ａ(7)＝ｂａ（7）＋ｃａ（7）＋ｄａ（7）＝１８＋１８＋１８＝５４となる。

答：５４通り

---

（参考問題の漸化式から一般項を求める）

上記図より、ba(n)＝ｃa(n)＝ｄa(n)（＝ｐ（n）とおく）、ａｂ(n)＝ａｃ(n)＝ａｄ(n)（＝ｑ（n）とおく）、およびそれ以外（すべて等しくｒ（n）とおく）の３種類に分かれます。

これから、ｐ（n）、ｑ（n）、ｒ（n）に関する漸化式、初期値は次の通りになります。

ｐ（n＋１）＝２×ｒ（n）　　・・・　（１１） ｑ（n＋１）＝２×ｐ（n）　　・・・　（１２） ｒ（n＋１）＝ｑ（n）＋ｒ（n）　・・・　（１３）

ｐ（１）＝０ ｑ（１）＝１ ｒ（１）＝０

（１１）より、ｒ（n）＝1/2×ｐ（n＋１）、ｒ（n＋１）＝1/2×ｐ（n＋２）、
（１２）より、ｑ（n）＝２×ｐ（n−１）となるので、これらを（１３）に代入して
　　1/2×ｐ（n＋２）＝２×ｐ（n−１）＋1/2×ｐ（n＋１）
ｎをｎ＋１に置き換え整理して、
　　ｐ（n＋３）−ｐ（n＋２）−４×ｐ（n）＝０　を得る。

前述の補題より、まずx³−x²−4=0を解きます。
（x−２）×（x²＋x＋２）＝０となり、x＝２、x＝（−１±√７ｉ）／２が得られます。
α＝（−１＋√７ｉ）／２、β＝（−１−√７ｉ）／２とおけば、
　　ｐ（n）＝Ａ×３^n-1＋Ｂ×α^n-1＋Ｃ×β^n-1が得られます。
Ａ、Ｂ、Ｃはｐ（１）＝Ａ＋Ｂ＋Ｃ＝０、ｐ（２）＝３Ａ＋αＢ＋βＣ＝０、ｐ（３）＝９Ａ＋α²Ｂ＋β²Ｃ＝２より、
　Ａ＝1/4、Ｂ＝（−７＋５√７ｉ）／５６、Ｃ＝（−７−５√７ｉ）／５６
を得ます。

よって、ａ（n）＝３×ｐ（n）
＝3/4×３^n-1＋3/56×（-7+5√7ｉ）×（（-1+√7ｉ）/2）^n-1＋3/56×（-7-5√7ｉ）×（（-1-√7ｉ）/2）^n-1

　　　　となります。

以上

---