第５９問の解答

１．問題　［場合の数］

　図１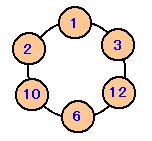
問題図		 図２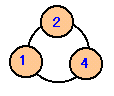
参考図
正の整数を６個選んで図１のように円周上に並べます。この６個の整数から連続したいくつかの整数を選んで、その和を計算します。最初に整数を上手に選んで、計算した和が１、２、・・と順番にできるだけ多くの連続した整数となるようにしたいと思います。
さて、最高いくつまでの連続整数を作ることができるでしょうか？

（整数が３個の場合は、図２のように７が最高です。）

２．解答例1（わかさひ君、ありさのお父さん、Nagahiroさん、戸村伸一さん他）

連続した整数を選ぶことが何通りできるか数えてみましょう。

参考図２

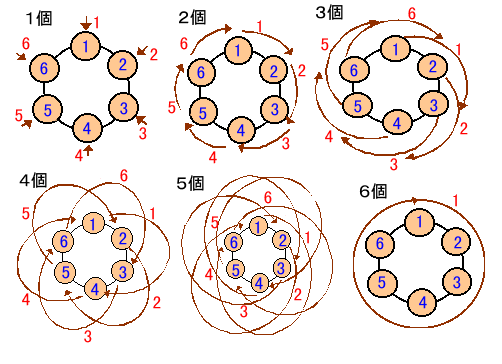
連続した整数の個数が１〜５のときは１、２、３、４、５、６から続く６通りづつ選べるが、６個全て選ぶのは１通りのみ。従って、全部で６×５＋１＝３１通りである。

ところで、現実に１〜３１までの整数を下図のように作ることができるので、最高は３１と分かる。

参考図３

　答：３１

以上

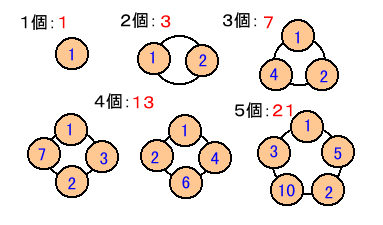
（参考）一般に整数の個数がｎのとき

ｎ＝６のときと同様に、ｎ×（ｎ−１）＋１が最大、ｎ＝１〜５のとき、
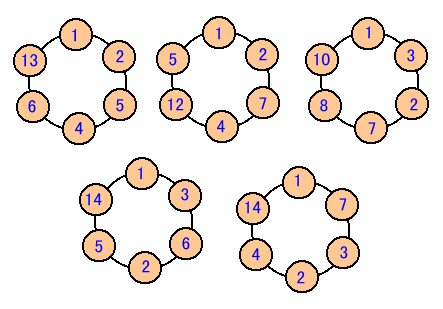
ｎ＝１・・・１個、ｎ＝２・・・２個、ｎ＝３・・・７個、ｎ＝４・・・１３個、ｎ＝５・・・２１個
と考えられるが、それを実現する並び方を下図に示す。

参考図３

なお、ｎ＝７のときは４３個が最大と考えられるが、現在のところ残念ながらこれを実現する並べ方は見つかっていない。３９個が最大のようである。

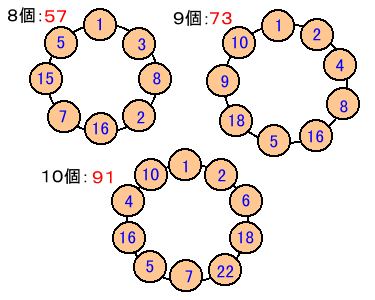
ところが、ｎ＝８、９、１０のときは、ｎ×（ｎ−１）＋１が最大となる並べ方が、それぞれ６通り、４通り、６通り見つかっており、下図にこれらの例を示す。

参考図４

以上

（参考２）シンガーの定理・・・ａｌｅｐｈさんによる
有限射影平面πについて、１本の直線の「結合」する点の個数をｎ＋１とすると
π上にはちょうどｎ^2＋ｎ＋１個の点とｎ^2＋ｎ＋１本の直線が存在する。

射影平面とは次の公理を満たす非ユークリッド的な平面。
＜公理１＞任意の異なる２個の「点」はちょうど１本の「直線」を「結合」する。
＜公理２＞任意の異なる２本の「直線」はちょうど１個の「点」を「結合」する。
＜公理３＞どの３個の「点」も同一の「直線」を「結合」しないような
４個の「点」が存在する。

＊「結合」は「通る」とか「含む」とかと考えてかまいません。

「点」と「直線」をこの公理に当てはまるようにうまく定義できれば
上の定理が適用できますね。