第６０問の解答

１．問題　［速さ］

　数Ｋｍ離れたＡ，Ｂ間をＴＯＲＡさんとマサル君が繰り返し往復しています。ＴＯＲＡさんはＡを、マサル君はＢを同時に出発したところ、１回目にすれ違ったのは１時間後、２回目にすれ違ったのはＡＢの中間点、３回目にすれ違ったのはＡから３Ｋｍの場所でした。

ＴＯＲＡさんのほうがマサル君より早く走れるとして、
（１）ＡＢ間の距離は何Ｋｍ？
（２）ＴＯＲＡさんがマサル君をはじめて追い越したのは、出発から何分後でしょうか？

２．解答例1（ありさのお父さん、中村明海さん他）

問題をダイアグラムとして図示すると次のようになります。

参考図１

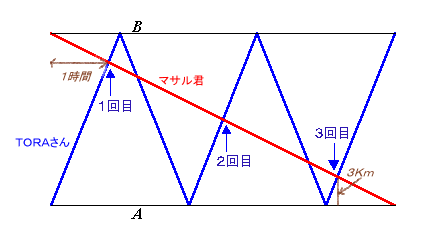
　出発して２回目にすれ違うまでにＴＯＲＡさんはＡＢ間を１往復半します。そこは、ＡＢの中間点ですから、そこから同じ時間走るとＢに到着します。同じ時間にマサル君はＡＢの半分づつ走るのでＴＯＲＡさんがＢに到着するのと同時にＡに着きます。


　以上のことから、上図ダイアグラムは１８０度回転すると元と重なるようになります。
従って、１回目にすれ違った点とＢとの距離は、３回目にすれ違った地点とＡとの距離に等しい３Ｋｍと分かります。

　次に、出発から２回目にすれ違うまでＴＯＲＡさんはＡＢ間を１往復半、マサル君はＡＢの半分走ることから、ＴＯＲＡさんとマサル君の速度比は２．５：１＝５：１と分かります。

　すると、出発から１回目にすれ違うまでの１時間にマサル君はＢから３Ｋｍ走るので、ＴＯＲＡさんは５倍の１５Ｋｍ走ることになり、ＡＢ間の距離は３＋１５＝１８Ｋｍとなります。

参考図２

　１回目にすれ違う点をＰ、ＴＯＲＡさんがマサル君をはじめて追い越す点をＱとします。
ＴＯＲＡさんがＰからＢまでを往復し、さらにＰからＱへ行くまでにマサル君がＰからＱへ行く距離の５倍を走るので、ＢＰ：ＰＱ＝２：１となります。マサル君はＢＰを１時間かけて走るので、ＰＱはその半分の３０分かかります。従って、ＢＱ間を合計９０分かけて走ることになります。

　答：（１）１８Ｋｍ　（２）９０分

以上

３．解答例２

方程式で解いてみます。

出発から１回目、２回目、３回目にすれ違うまでの時間をｔ１、ｔ２、ｔ３時間、Ｑにつく時間をｔ４、マサル君とＴＯＲＡさんの走る速度をｖ１、ｖ２Ｋｍ／ｈ、ＡＢ間の距離をｄＫｍとします。

次の式が成り立ちます。

(v1+v2)*t1=d　　 ・・・　(1)
v1*t2=d/2　　　　 ・・・　(2)
v2*t2=２．５*d　　・・・　(3)		 (v2*t3-4*d)+v1*t3=d　・・・　(4)
(v2*t3-4*d)=3　　　　　 ・・・　(5)
v1*t4=v2*t4-d　　　　　・・・　(6)

これを解くと、t1 = 1, t2 = 3,t3 = 5, t4 = 1.5,v1 = 3, v2 = 15, d = 18を得ます。

以上