第63問の解答
1.問題 [空間図形]
| 面積が216cm2の2等辺3角形の紙があります。そこから第1図のように、直角2等辺3角形を切り取り、これ上手にたたむと図2のような3角錐が出来ました。(底面:直角2等辺3角形、側面:直角3角形×2,2等辺3角形) では、この3角錐の体積は何cm3でしょう? |
第1図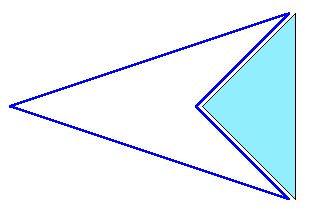 |
第2図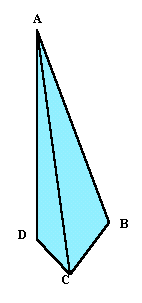 |
2.解答例1(Nagahiro、Y.さん、alephさん他)
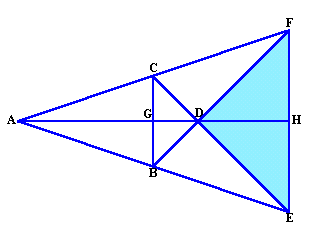
そこで、下図のように補助線を引きます。E、Fが3角錐の頂点Aと重なるようになるので、BはAEの中点、CはAFの中点、△BDC、△EDFは直角2等辺3角形になります。
従って、△ABCと△AEFは相似な2等辺3角形で相似比は1:2。
よって、CG=1とおくと、FH=2,GD=CG=1、FH=FH=2。
GH=GD+DH=3、よってAG=DH=3。△ABCの面積=△AEFの面積×1/4=216×1/4=54cm2。
AG:GD=3:1なので△BDCの面積=△ABCの面積×1/3=18cm2。
よって、CDを1辺とする正方形の面積=△BDCの面積×2=36cm2。
従って、CD=6cm。DF=CD×2=12cm。三角錐の体積=△BDC×DF×1/3=18×12×1/3=72cm3。
第3図
答:72cm3
以上