第６６問の解答

---

１．問題　［時計算］

図１

図２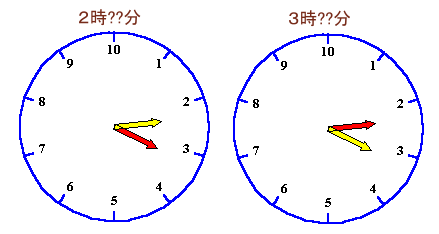

図１のような１日が２０時間、１時間が７２分という奇妙な時計があります。そのうえ、時針と分針の長さ、色が等しいのでその区別がつきません。 ほとんどの時刻は針の角度から時刻を推測できます（図１の場合は２時３６分）が、中には推測できない時刻もあります。（図２の場合、ただし区別するため時針：黄色、分針：赤色にしている） この時計で推測できない時刻は１日の中で何回あるでしょうか？

---

２．解答例1（長野　美光さん、中村明海さん他）

Ｘ時○○分と、Ｙ時××分において、時針と分針がちょうど入れ替わる位置に
来る時刻が１つ存在します。
ただし、Ｘ＝Ｙのときは、針が重なるので時刻は判明するので除きます。

従って、１つのＸ時に対し、題意のような時刻は１０−１＝９回存在します。

よって、判別できない時刻は午前１０×９＝９０回、午後も同じ９０回、合計１日１８０回です。

答：１８０回

以上

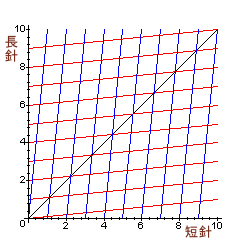
（参考）時針、分針を表すグラフ 交点が判別できない時刻になります。 （ｙ＝ｘとなるときを除く）

---