第６７問の解答

---

１．問題　［推理算］

左図のように８チームが参加してトーナメント試合を行いました。引き分けはありません。 表はトーナメント終了後における各チームの総得点、総失点の集計表です。ただし、空欄は不明です。 これから決勝戦の結果は、「○チームが×チームに**：**で勝った」のかを考えて下さい。

---

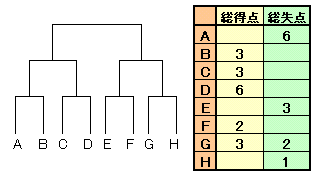２．解答例1

（右のブロック）

総得点、総失点とも分かっているＧチームに着目して、まず右のブロックを考えます。
Ｇチームは総得点が総失点より多いので、１回戦敗退はあり得ません。すると、対戦相手のＨチームの負けと分かります。 すなわち、Ｇ対Ｈチームは１対０でＧチームの勝ちです。

従って、Ｇチームの残り試合の総得点、総失点ともに２点となるので、Ｇチームは２回戦敗退はあり得ません。すなわち、決勝戦の一方はＧチームとなります。

さて、Ｅ対Ｆチームはどうでしょうか。Ｅチームの総失点がＦチームの総得点より多いので、Ｆチームの勝ちはあり得ません。従って、Ｅ対Ｆチームは３点以上対２点でＥチームの勝ち。
ところで、既にＧチームが決勝戦進出と分かっていますので、２回戦のＥ対ＧチームはＧチームの勝ち。
結果は１対０となります。

以上から、決勝戦は１対２でＧチームの負けと分かります。

ここまでの結果をトーナメント表等に表しておきます。

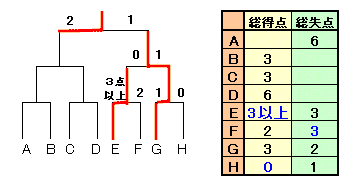
（左のブロック）

Ｃ対Ｄチームを考えます。Ｄチームの総得点のほうがＣチームより多いので、４点以上対３点でＤチームの勝ち。
Ｄチームの残り試合の総得点は２点以下となるので、２回戦を勝って決勝戦進出はあり得ません。（決勝戦で２点入れているから、２回戦が０点となる）

次にＡ対Ｂチームを考えます。Ａチームの総失点のほうがＢチームの総得点より多いので、４点以上対３点でＡチームの勝ち。

従って、決勝戦進出はＡチームとなります。

以上から、決勝戦は「Ａ対Ｇチームの対戦となり、２対１でＡチームの勝ち」となります。

残りの得失点を推定すると下表のようになります。

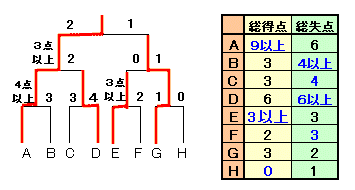
以上

---