第６８問の解答

１．問題　［平面図形］

問題図
左図のように、三角形ＡＢＣの底辺ＢＣを４等分し、ＡＢＣの面積の２分の１の大きさのＰＢＦとＡＢＣの大きさの３分の１の大きさのＱＥＣの２つの三角形を描きました。

このとき、ＡＢＣの面積はＲＥＦの面積の何倍になるでしょうか？

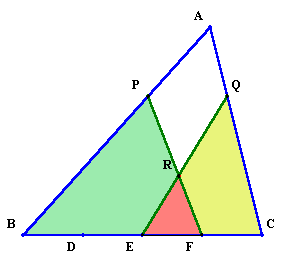２．解答例1（DrKさん他）

参考図１

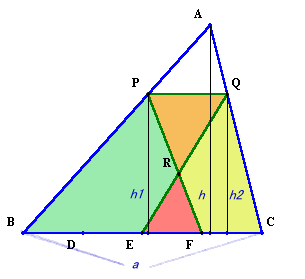
底辺ＢＣの長さをａ、三角形ＡＢＣ、ＰＢＦ、ＱＥＣおよびＲＥＦの高さをそれぞれｈ、ｈ１、ｈ２、ｈ３とする。

題意から、
　1/2×（3/4×ａ）×ｈ１＝（1/2×ａ×ｈ）×１／２、
　1/2×（2/4×ａ）×ｈ１＝（1/2×ａ×ｈ）×１／３。
よって、ｈ１＝ｈ２＝2/3×ａ。

これから、ＰＱはＢＣと平行となるので、三角形ＡＰＱとＡＢＣおよび三角形ＲＰＱとＲＦＥは相似となる。

ｈ１：ｈ＝２：３より、ＰＱ：ＢＣ＝１：３、ＰＱ＝ａ／３。
ＥＦ：ＰＱ＝ａ／４：ａ／３＝３：４、よってｈ３＝３／７×ｈ１＝２／７×ｈ。

従って、ＲＥＦの面積＝1/2×（1/4×ａ）×（2/7×）ｈ＝（1/2×ａ×ｈ）×１／１４。

よって、ＡＢＣの面積はＲＥＦの面積の１４倍となる。

答：１４倍

以上

３．解答例1（CRYING DOLPHINさん他）

ＰＱとＡＢが平行でないとき（例えばｈ１＞ｈ２とする）には、次のようにして求まります。

参考図２

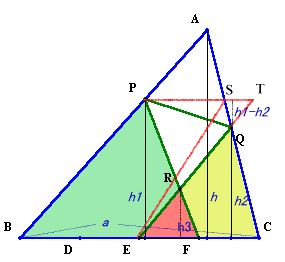
点Ｐを通りＢＣに平行に直線を引き辺ＡＣとの交点をＳ、ＥＱの延長線との交点をＴとする。

解答例１と同様、三角形ＡＰＳとＡＢＣが相似で相似比が（ｈ−ｈ１）：ｈであることから、
　ＰＳ＝ａ×（ｈ−ｈ１）／ｈ。

また、三角形ＱＳＴとＱＣＢが相似で相似比が（ｈ１−ｈ２）：ｈ２であることから、
　ＳＴ＝ａ／２×（ｈ１−ｈ２）／ｈ２。

さらに、三角形ＲＰＴとＲＥＦが相似で相似比がＰＴ：ＥＦであることから、
　ｈ３＝ｈ１×ＥＦ／（ＰＴ＋ＥＦ）
　　　＝ｈ１×1/4×ａ／（ａ×（ｈ−ｈ１）／ｈ＋ａ/2×（ｈ１−ｈ２）／ｈ２＋1/4×ａ）
　　　＝ｈ１×ｈ２×ｈ／（（２×ｈ１＋３×ｈ２）×ｈ−４×ｈ１×ｈ２）。

よって、三角形ＡＢＣの面積／ＲＥＦの面積
　　　＝（ＢＣ／ＥＦ）×（ｈ／ｈ３）
　　　＝４×（（２×ｈ１＋３×ｈ２）×ｈ−４×ｈ１×ｈ２）／（ｈ１×ｈ２）。

ここで、ｈ１＝ｈ２＝２／３×ｈとすると、上記比は、
　　　　４×（５×２／３−４×２／３×２／３）／（２／３×２／３）
　　　＝５×２×３−４×２×２＝１４。

以上