第６９問の解答

１．問題　［流水算］

問題図 問題図２
図のように、Ａ、Ｂ、Ｃの３カ所に区切ってある水槽のＡの部分に一定の割合で水を注いでいきます。

このときの、Ａでの水面の高さと入れはじめてからの時間の関係を表したグラフの中でＸにあてはまる数値を求めて下さい。

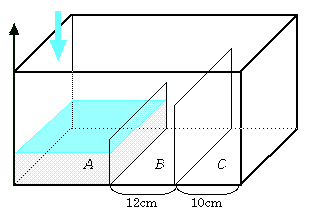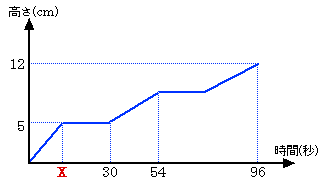２．解答例1（中村明海さん、おりくん、CRYING DOLPHINさん他）

参考図１

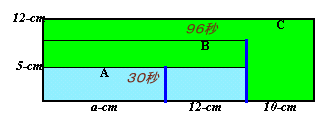
水槽の奥行きは一定なので、注がれた水の体積は、側面の面積に比例する。
Ａの部分の底の長さをａとする。

題意から、５×（ａ＋１２）：１２×（ａ＋２２）＝３０：９６。
　よって、（ａ＋１２）：（ａ＋２２）＝３：４。
これから、（ａ＋２２）−（ａ＋１２）＝１０ｃｍを１とすると、ａ＋１２は３、すなわちａ＋１２＝３０ｃｍ、ａ＝１８ｃｍ。

ａ＋１２＝３０ｃｍの部分に高さ５ｃｍまで水を注ぐのに３０秒かかるのだから、ａ＝１８ｃｍのＡの水槽をいっぱいにするにはには１８秒かかることとなる。

答：１８秒

以上

３．解答例２（EGUCHIさん、ｋｕｒｉ他）

解答例１と同様、側面の面積で考えます。高さ５ｃｍの長方形ＪＦＬＮに対し３０秒かかるのだから、同じ底辺で高さ１２ｃｍの長方形ＥＦＬＱに対しては３０×１２／５＝７２秒かかります。

参考図２

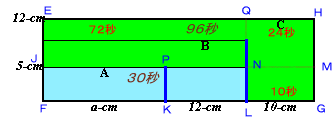
すると、ＱＬＧＨに対しては９６−７２＝２４秒かかることになります。
よって、高さ５ｃｍの交点をＮＬＧＭでは２４×５／１２＝１０秒となります。

従って、同じ高さ５ｃｍのＰＫＬＮでは１２秒、Ａの水槽ＪＦＫＰでは３０−１２＝１８秒かかることになります。

以上