第７２問の解答

１．問題　［平面図形］

問題図 　
左図は、一辺が８ｃｍの正方形の一つの隅を折り返したときのものです。

青色の部分の面積を求めて下さい。

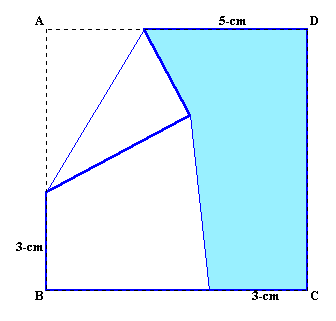２．解答例1：（ありさのお父さん、ＪＩＲＯさん他）

参考図

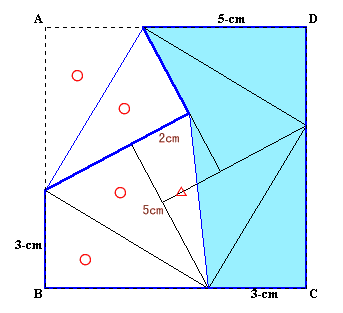
　四隅から折り返すと、○印のものとと合同な直角三角形が８個と真ん中に一辺が２ｃｍの正方形が１個できます。

　元の正方形から求める面積を除いた面積は、○印の直角三角形４個△印の直角三角形１個の面積の和＝（１／２×３×５）×４＋１／２×２×５＝３５ｃｍ2となる。

　よって、求める面積＝８×８−３５＝２９ｃｍ2

答：２９ｃｍ2

以上

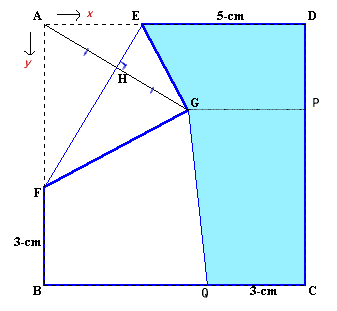
３．解答例２：（長野美光さん他）

下図より、ＡＨ＝ＨＧ、ＥＦとＡＧは直交することが分かる。

参考図２

Ａを原点とし、ＡＤ方向をＸ軸、ＡＢ方向をｙ軸とする座標系で考えます。

ＥＦ：ｘ／３＋ｙ／５＝１、ＡＨ：３・ｘ−５・ｙ＝０より、Ｈの座標は、（75/34,45/34）、従って、Ｇは（75/17,45/17）と分かります。

これより、
ＧＰ＝８−７５／１７＝６１／１７、ＤＰ＝４５／１７，ＰＣ＝８−４５／１７＝９１／１７。

よって、求める面積
＝１／２×（５＋６１／１７）×４５／１７＋１／２×（６１／１７＋３）×９１／１７
＝２９ｃｍ2