第７４問の解答

---

１．問題　［場合の数］

左図のように、円周上に５個の点をとってそれぞれの点をすべて線で結びます。 円の内部ではどの３直線も１点で交わることがないように結べば、円は１６個の領域に分割されます。 これと同じように円周上に８個の点を取りそれぞれを結んだ場合、円周はいくつの領域に分割されるでしょうか。

---

２．解答例1：（ありさのお父さん他）

円周上の点がｎ個のときの領域数をＳ_nとします。Ｓ₁＝１は明らか。
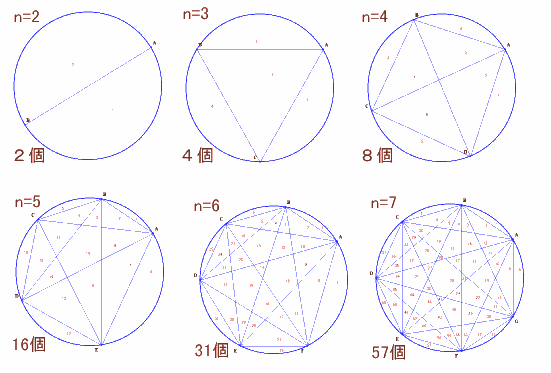
Ｓ₂・・Ｓ₇は下図の通り。

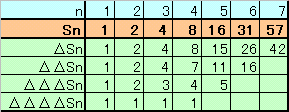
　ここで、Ｓ_nの階差を求めると、第４階差が常に１となり、ΔＳ₇＝４２と見込まれるので、Ｓ₈＝５７＋４２＝９９、一般にＳ_nはｎの４次式で表されると予想される。

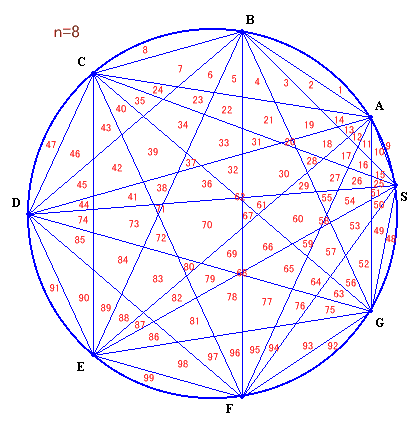
実際、ｎ＝８のときの図は下記のとおりである。

答：９９個

以上

---

３．解答例２：（B2さん、ｋｕｒｉ他）

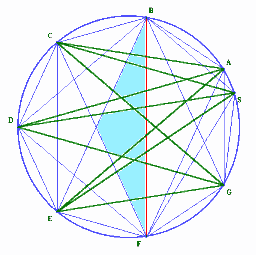
ΔＳ_ｎを求めてみよう。下図ではＦＢの左に点が３個、右に３個あるので３×３＝９個の直線があり、これらとＦＢの交点は９個、増える領域数は９＋１＝１０個となっている。
同様にして、ｎが１増えたときの領域数の増分は、新たな点と元のｎ個の点を結んだときの直線との交点数＋１の合計となることが分かる。

従って、
ΔＳ_ｎ＝Σ(k=１,n){(k-1)(n-k)+1}=Σ(k=0,n-1){k・(n-k-1)+1}
　　　＝(n-1)Σ(k=0,n-1)k−Σ(k=0,n-1)k²＋ｎ
　　　＝(n-1)(n-1)n/2−(n-1)n(2n-1)/6＋ｎ
　　　＝n(n²-3n+8)/6

Ｓ(n)＝Σ(k=1,n-1){k(k²-3k+8)/6}+Ｓ(1)
　　　＝（Σ(k=1,n-1)k³−３Σ(k=1,n-1)k²＋８Σ(k=1,n-1)k）／６＋１
　　　＝[{(n-1)n/2}²−3(n-1)n(2n-1)/6＋8(n-1)n/2]／６＋１
　　　＝(n⁴-6n³+23n²-18n+24)/24

これより、Ｓ(8)＝(８⁴-6・８³+23・８²-18・８+24)/24 =99。

---

３．解答例２：（あれふさん、たなかさん他）

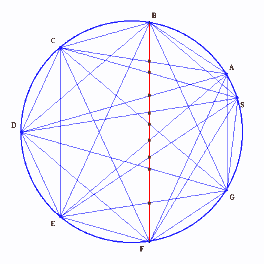
順に線を引いていくと考えて円の内部の増え方は
（１）他の線分と交わる毎に１つ増える。
（２）線分を引き終えると１つ増える。

最初(線を引く前）円の内部は１つですから結局円の内部は
　　１＋交点の数＋線分の数＝１＋ｎＣ４＋ｎＣ２
＝１＋n(n-1)(n-2)(n-3)/24+n(n-1)/2＝(n⁴-6n³+23n²-18n+24)/24
に分けられます。

---