第７５問の解答

１．問題　［差集め算］

問題図

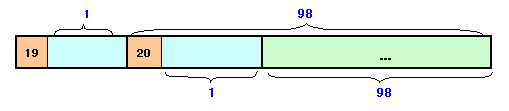
ある小学校では、卒業生に鉛筆を配ることにしました。
１人目には１９本と残りの１／９９を渡し、２人目には２０本と残りの１／９９を、３人目には２１本と残りの１／９９を・・・というように規則正しく渡していきました。
すると、用意した鉛筆を余すことなく全員がちょうど同じ本数だけもらえたことになりました。

では、全部で用意した鉛筆の本数は何本あったのでしょうか。

２．解答例1：方程式を解く（ありさのお父さん、EHさん、domodomさん他）

（ありさのお父さん、ＥＨさん）

ｘ＝鉛筆の本数合計−１９とします。

参考図

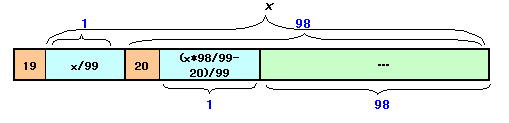
１９＋ｘ／99＝２０＋(ｘ*98/99-20)／99よりｘ＝7821を得る。
よって、鉛筆の本数合計＝ｘ＋１９＝７８４０。

（ｄｏｍｏｄｏｍさん、ｋｕｒｉ）

１人目の１９本以外の本数をｘ本、２人目の２０本以外の本数をｙ本とします。

参考図２

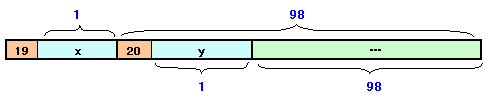
　１９＋ｘ＝２０＋ｙ　　　　・・・　（１）
　９８ｘ＝２０＋ｙ＋９８ｙ　・・・　（２）

（１）より、ｘ＝ｙ＋１。
（２）に代入して、９８（ｙ＋１）＝２０＋９９ｙ、
よって、ｙ＝７８、ｘ＝７９
従って、全ての本数＝１９＋９９ｘ＝７８４０本と分かります。

答：７８４０本

以上

３．解答例２：規則性に着目（長野美光さん、中村明海さん、みのちゃん、たなかさん他）

参考図３

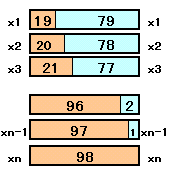
卒業生の人数をｎ人とする。各人がもらう鉛筆のうち、１本ずつ増えていく方をｘk本、残りをｙk本とする（ただし、１≦ｋ≦ｎ）。各人がもらう本数は皆同じだから、ｙkは１本ずつ増えていくことになる。
ｘk+1＝ｘk＋１、ｙk+1＝ｙk−１（ただし、１≦ｋ≦ｎ−１）

すなわち、ｘ1＝１９、ｘ2＝２０、・・・、ｘn＝１８＋ｎ、

最後の人（ｎ人目）は、残りがもうないのでｙn＝０。
よって、ｙn-1＝１となりｙn＝９８×ｙn-1＝９８。

従って、各人がもらう鉛筆は９８本づつと分かります。

最初の人を考えると、ｘn＋ｙn＝９８、ｙn＝０より、ｘn＝１８＋ｎ＝９８、
よって、ｎ＝９８−１８＝８０人。

従って、鉛筆合計は、９８本×８０人＝７８４０本となります。