第７６問の解答

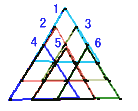
１．問題　［場合の数］

問題図
左図のように２１個の点が等間隔に並んでいます。
このうち、３個の点をとって正三角形となるような、３個の点の選び方は何通りあるでしょう。

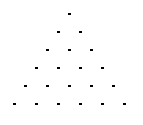２．解答例1：

対象性より、正三角形となるように３個の点を選べば、各点を辺上に持つような正三角形が１個存在します。下図は、外側の正三角形の辺の長さがＬ＝３のときの例です。

参考図

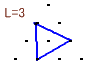
Ｌ＝１、・・５について、このような正三角形が何種類あるか調べてみましょう。

参考図２

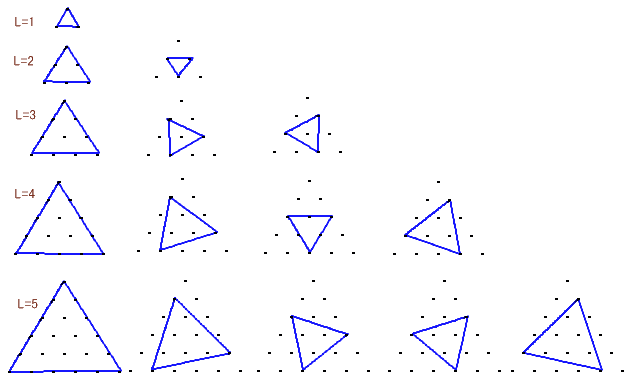
上図から、Ｌと同じ数だけの種類の正三角形があることが分かります。

次に、各Ｌについて、外側の正三角形が全部で何個あるかを考えてみましょう。
下図はＬ＝３の場合です。
頂点が何個あるかを数えればいいので、この場合は１＋２＋３＝６通りあります。

参考図３

同様にして、
　Ｌ＝１のとき、１＋２＋３＋４＋５＝１５通り、
　Ｌ＝２のとき、１＋２＋３＋４　　＝１０通り、
　Ｌ＝３のとき、１＋２＋３　　　　＝　６通り、
　Ｌ＝４のとき、１＋２　　　　　　＝　３通り、
　Ｌ＝５のとき、１　　　　　　　　＝　１通り、　　合計３５通りあります。

従って、求める３個の点の選び方は、１５×１＋１０×２＋６×３＋３×４＋１×５＝７０通りあることが分かります。

答：７０通り

以上

３．解答例２：一般解

一般に、元の正三角形の辺にある点がｎ個の時、求める正三角形を成す３点の選び方はａn＝n+2C4通りである。

本問題の場合は、n=６の場合で、6+2C4＝８×７×６×５／４×３×２×１＝７０通りである。

（証明１）

解答例１と同様に、
ａn＝Σ［（Ｌ=1,n-1）Ｌ×Σ(ｋ=1,n-Ｌ)Ｋ］
従って、
ａn＝Σ［（Ｌ=1,n-1）Ｌ（n-Ｌ）(n-Ｌ+1)/２］
　　＝［n(n+1)Σ(Ｌ=1,n-1)Ｌ−(2n+1)Σ(Ｌ=1,n-1)Ｌ2＋Σ(Ｌ=1,n-1)Ｌ3］/２
　　＝［n(n+1)(n-1)n−(2n+1)(n-1)n(2n-1)/6＋(n-1)2n2/4］/２
　　＝(n+2)(n+1)n(n-1)/24
　　＝n+2C4

（証明２）サトラさんによる

参考図４

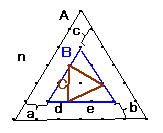
「方針」：一番外側の正三角形（以下、正三角形Aと呼びます）に各辺が平行な正三角形（以下、正三角形Bと呼びます）を1つ決め、 正三角形Bの周上に３つの頂点をもつ正三角形（以下、正三角形Cと呼びます）を１つ決めるという選び方の場合数を求めます。

「詳細」：
正三角形Aの左辺からa回、下の辺からb回、右辺からc回、内側に向かって平行に狭めていくと、各辺に（n-a-b-c）点含まれる正三角形Bが１つ決まります。
ただし、あたりまえですが、a>=0,b>=0,c>=0,a+b+c=<n-2 になるようにします。

正三角形Bの下辺の１点を正三角形Cの１頂点に選べば他の辺上の頂点も自動的に決まり、正三角形Cが１個決まります。（下辺での選択可能な点は一番左端から(n-a-b-c-1)個とし、一番右の点は右辺から選ぶ点と決め、下辺での選択肢に入れません。）

左端からd回（但し、o=<d=<n-a-b-c-2 ）右側に行った点を正三角形Cの１頂点に決めると、正三角形Bの下辺で、正三角形Cの頂点より右に（n-a-b-c-d-2）点あります。（一番右端は除く。）

そこで、e=n-a-b-c-d-2 と 置くことにします。 当然、0=<e かつ、a+b+c+d+e=n-2 となります。

以上の条件を満たすようにa〜eを選べば、ちょうど１個正三角形が決まり、 また、すべての正三角形は上記の方法で選ぶことができます。

そこで、白石a個、黒石1個、白石b個、黒石1個、白石c個、黒石1個、白石d個、黒石1個、白石e個を（石の数は合計n-2+4=n+2個）ならべておく（つまり 1〜n+2の中の４つを選んで黒石にする）場合の数と、正三角形の数は等しいことがわかり、n+2C4個となります。