第７７問の解答

---

１．問題　［平面図形］

左図は、半径が６ｃｍで円の４分の１の扇形ＯＡＢを、Ｏを中心としてＯＡ2Ｂ2の位置まで５０度回転させたものです。 ＡとＢ2、Ａ2とＢを結んだときに得られる緑色の部分の面積を求めて下さい。

---

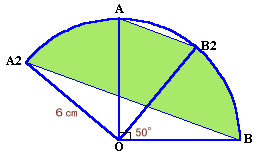２．解答例1：

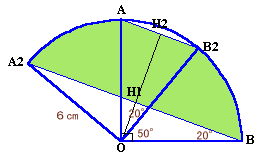
Ａ2Ｂの中点をH1、Ａ2Ｂ2の中点をH2とします。

∠ＢＯＡ2＝９０＋５０＝１４０°、よって∠ＯＢＨ1＝９０−∠ＢＯＡ2／２＝２０°。
∠Ｂ2ＯＨ2＝∠Ｂ2ＯＡ／２＝（９０−５０）／２＝２０°。

従って、△Ｂ2ＯＨ2、△ＯＢＨ1は、ともに斜辺が６ｃｍで、一つの角が２０度の直角三角形となり合同。
よって、△Ａ2ＯＢ=△ＯＢＨ1×２＝△Ｂ2ＯＨ2×２＝△ＡＯＢ2

求める面積＝（扇形Ａ２ＯＢ−△Ａ2ＯＢ）−（扇形ＡＯＢ2−△ＡＯＢ2）
　　　　　　　＝（扇形Ａ２ＯＢ−扇形ＡＯＢ2）−（△Ａ2ＯＢ−△ＡＯＢ2）
　　　　　　　＝（π×６²×１４０／３６０−π×６²×１４０／３６０）
　　　　　　　＝π×６²×１００／３６０＝３．１４×３６００／３６０
　　　　　　　＝３１．４ｃｍ²

答：３１．４ｃｍ²

以上

---