第７９問の解答

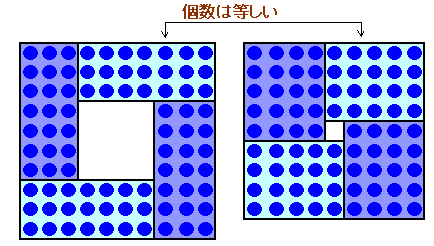
１．問題　［場合の数］

問題図
左図のように、幅が２の正方形の形に碁石を並べたものを２列の中空方陣と呼びます。

今、ここに何個かの碁石があります。
この碁石を全部使って３列の中空方陣を作るときと４列の中空方陣を作るときでは、外側の１列に並ぶ碁石の数が１０個違ってきます。
碁石は全部で何個あるのでしょう？

２．解答例1：（ぱたさん）

参考図

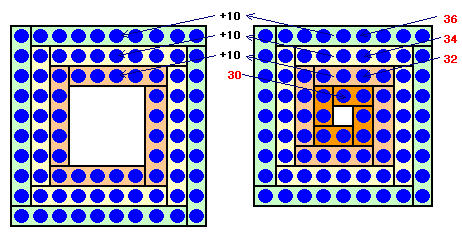
正方形の周囲の碁石の数は、一辺にある碁石数の４倍になることに注目します。
また、中に入るごとに一返にある碁石数は２個ずつ減っていきます。

図より、３列と４列の中空方陣の外側の３列で一辺にある碁石数は延べ３０個の差ができます。
従って、４列の中空方陣の最も内側の一辺にある碁石数は３０個と分かります。

これから４列の中空方陣の一辺にある碁石数は、順に３２個、３４個、３６個となります。

これより、中空方陣の合計碁石数は（３０＋３２＋３４＋３６）×４＝５２８個と求められます。　　　　

答：５２８個

以上

３．解答例２：（こだまさん、Miki Sugimotoさん、T.Endさん他）

中空方陣を４つの合同な長方形に分割して考える。

参考図２

碁石の合計数が等しいことから、これらの長方形の中の碁石数も等しいことになる。

ところで、長方形の横の長さは１０＋１＝１１個分だけ３列の中空方陣の方が長いので、
これをｎとすると、３×ｎ＝４×(ｎ−１１)となり、ｎ＝４４が得られます。

従って碁石の合計数は、３×４４×４＝５２８個と分かります。

４．解答例４：（こだまさん、ｋｕｒｉ他）

中空方陣の碁石数合計は、正方形の面積から中空部分の正方形の面積を除いたものとなる。

従って、３列の中空方陣で外側の１列にある碁石数をｎとすると、
　ｎ2−（ｎ−６）2＝（ｎ−１０）2−（ｎ−１８）2　より、ｎ＝４７を得ます。

よって、碁石数合計は４７2−（４７−６）2＝５２８個と分かります。