第８１問の解答

---

１．問題　［平面図形］

左図のような半径９ｃｍの円盤と、一番長い辺の長さが１８ｃｍの三角定規を用意します。これを最初左図のように配置し、三角定規を毎秒１ｃｍの速さで半円盤の後ろをまっすぐに通過させ、半円盤にさえぎられることなく見える部分の面積変化を調べます。 動かし始めて９秒後の面積をＳ9、１８秒後の面積をＳ18とするときＳ9はＳ18の何倍になりますか？

---

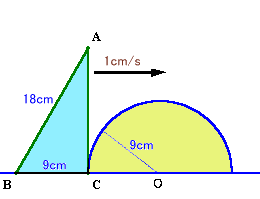２．解答例1：（Tak'SAkaiさん、popopoさん、イデムリンさん、大岡敏幸さん、DrKさん他）

　　９秒後は三角定規の頂点Ｃが円の中心Ｏの位置に、１８秒後はＢがＯの位置に来ます。

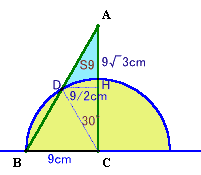
９秒後

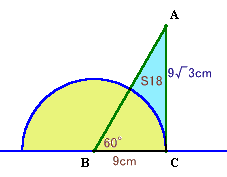
１８秒後

題意より∠ＡＢＣ＝６０度、∠ＡＣＢ＝９０度が分かります。
まず、Ｓ18＝△ＡＢＣ−中心角６０度の扇形となります。

次に１８秒後のとき辺ＡＢと円周の交点をＤとすると、△ＣＤＢは、ＣＢ＝ＣＤより２等辺三角形となります。
従って∠ＡＢＣ＝６０度より△ＣＤＢは正三角形と分かります。
よってＤＢ＝ＢＣ＝９ｃｍとなり、ＡＤ＝ＡＢ−ＤＢ＝１８ｃｍ−９ｃｍ＝ＤＢ。

以上から、△ＡＤＣ＝△ＡＢＣ×1/2。
よって、Ｓ9＝△ＡＤＣ−中心角３０度の扇形
　　　　　　＝△ＡＢＣ×1/2−中心角６０度の扇形×1/2
　　　　　　＝Ｓ18×1/2。

答：1/2倍

以上

---