第83問の解答
1.問題 [空間図形]
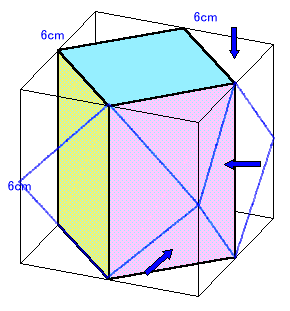
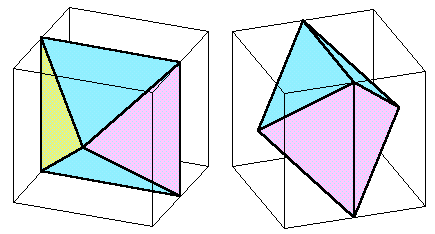
| 上図は、1辺が6cmの立方体の上面と下面の各辺の中点を通る平面で立方体の四隅を切り落としてできた直方体です。 左右の面および前後の面からも同様にして四隅を切り落としてできる立体の体積を求めて下さい。 |
2.解答例1:(たなかさん、ありさのお父さん、シイサンさん他多数)
上下、および左右から四隅を切り取った立体は下図のように底面が1辺6cmの正方形で高さ3cmの正四角錐を2個合わせた形となります。
従って、この立体の体積をV2、元の立方体の体積をV0とすると、
V0=6×6×6、V2=(6×6×3)×1/3×2=V0×1/3
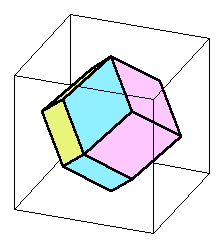
となります。さらに前後から四隅を切り取ると下図のような菱形12個の面からなる立体となります。
(参考)マウスでドラッグして下さい。
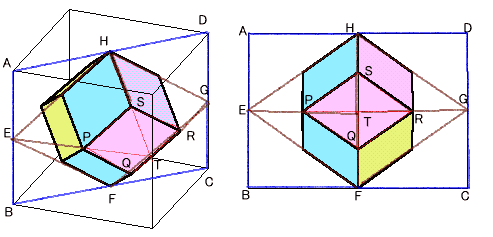
これを下図のように、上面および下面の対角線を通る平面で2つに分割すると、1つの切り取る立体TPQRS(四角錐)はTEFGHと相似で高さは半分、従って体積は1/8になります。
従って、求める12面体の体積をV3とすると、
V3=V2−(V2×1/2)×1/8×4=V2×3/4
となる。
以上から
V3=V2×3/4=V0×1/3×3/4=V0×1/4=54cm3となります。
答:54cm3以上
3.解答例2:(kuri他)
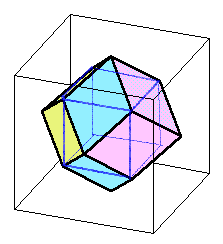
求める12面体は下図のように1辺が3cmの立方体1個と底面が1辺3cmの正方形で高さ1.5cmの正四角錐6個に分割されます。
従って、体積は3×3×3+(3×3×3/2×1/3)×6=27+27=54cm3となります。
以上