第８４問の解答

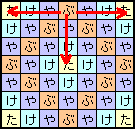
１．問題　［場合の数］

問題図
左図の中に「たけやぶやけた」と読むことができる並びは、何通りありますか？
ただし、同じ場所を２度通っても構いませんが、隣り合っていないマスに跳んではいけません。
また、同じルートを逆向きに読む場合は、別個に数えて下さい。

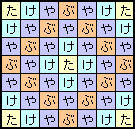２．解答例1：（みのちゃん、tomhさん他）「た」と「ぶ」に注目

「た」を出発して「ぶ」を経由して「た」に行くと考えます。

（１）角の「た」から「ぶ」を経由して真ん中の「た」に行く場合、
　　真ん中の「た」から「ぶ」を経由して角の「た」に行く場合

参考図１

　これは最短経路の進み方となるので、それぞれ
　　（３＋３）！／３！３！＝６×５×４／３×２×１＝２０通り

「た」と「た」の組み合わせは４×２＝８通りあるので、合計２０×８＝１６０通り


（２）角の「た」から「ぶ」を経由して元の角の「た」に戻る場合、
　　真ん中の「た」から「ぶ」を経由して真ん中の「た」に戻る場合

　「ぶ」への行ったあと、合い対する「た」に行くのと、元の「た」に戻る行き方は、対象性から同じなので、結局（１）の場合と同じそれぞれ２０通りあり、「た」と「た」の組み合わせも同じ８通りあるので、合計２０×８＝１６０通り。

ただし、真ん中の「た」から外側の「ぶ」を経由して元の「た」に戻る場合をダブルカウントしているので、この４通りを除く必要があるので、１６０−４＝１５４通り。


（３）角の「た」から同じ辺にある他の角の「た」に行く場合

「た」と「た」の組み合わせは８通りで、行き方はそれぞれ１通りだから合計８通り

以上から、１６０＋１５６＋８＝３２４通りと分かります。


答：３２４通り

以上

３．解答例２：（ありさのお父さん）「ぶ」に注目

各「ぶ」について，「ぶ」に到着する「たけやぶ」と「ぶ」から出発する「ぶやけた」
は同じ道を逆に見ているだけです。したがって，「ぶやけた」の数を数えて，
２乗すればよい。

（１）１列目の「ぶ」を経由する場合

参考図２

ひとつの「ぶ」に対して「ぶやけた」の数は ３個、「ぶ」の数は４個。
従って、３2×４＝３６通り。

（２）２列目の「ぶ」を経由する場合

参考図３

ひとつの「ぶ」に対して同じ「た」へ行くひとつの「ぶ」に対して「ぶやけた」の数は、最短経路となるので（１＋２）！／１！２！＝３通り。「た」は２組あるので合計６通り。

「ぶ」は合計８個あるので、６2×８＝２８８通り

以上から、３６＋２８８＝３２４通りとなります。

以上