第８５問の解答

---

１．問題　［平面図形］

左図でＡＢＣは直角２等辺三角形、ＭとＮはそれぞれＢＣ，ＡＭの中点、角ＢＰＣは９０度、ＢＣの長さは３０ｃｍになっています。 このとき、三角形ＰＱＭの面積は何ｃｍ2になりますか？

---

２．解答例1：

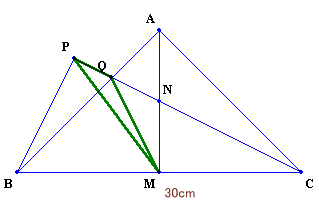
ＱからＢＣに下ろした垂線の足をＨ、ＭからＰＣに下ろした垂線の足をＲとする。

　まず、ＢＭ＝ＭＣ＝ＡＭ、ＡＮ＝ＮＭより、ＮＭ：ＭＣ＝１：２。

△ＮＭＣ、△ＭＲＣ、△ＮＲＭは全て相似なので、ＮＲ：ＲＣ＝１：４、
よって△ＮＲＭ：△ＭＲＣ＝１：４。

△ＮＭＣ＝ＮＭ×ＭＣ×1/2＝15/２×１５×1/2＝２２５／４。
よって、△ＭＲＣ＝△ＮＭＣ×4/5＝４５ｃｍ²。

△ＭＲＣと△ＢＰＣは相似で相似比は１：２、面積比は１：４。
よって、△ＢＰＣ＝△ＭＲＣ×４＝１８０ｃｍ²。

次に、△ＱＨＣと△ＮＭＣが相似、△ＱＢＨが直角２等辺三角形より、ＢＨ＝ＱＨ、ＢＨ：ＨＣ＝１：２。
よって、△ＱＢＣ＝ＢＣ×ＱＨ×1/2＝３０×１０×1/2＝１５０ｃｍ²。

従って、△ＰＱＢ＝△ＢＰＣ−△ＱＢＣ＝１８０−１５０＝３０ｃｍ²。

△ＰＭＱは△ＰＱＢと底辺ＰＱが共通で高さの比がＲＭ：ＰＢ＝１：２より
△ＰＭＱ＝△ＰＱＢ×1/2＝３０×1/2＝１５ｃｍ²。

答：１５ｃｍ²

以上

---