第90問の解答
1.問題 [推理算]
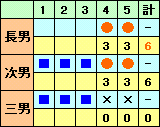
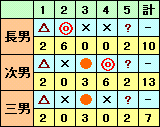
| 長男、次男、三男の3人がじゃんけんで得点を競うゲームをしました。 得点は、1回の勝負ごとに各自に与えられ、1人勝ちなら6点、2人勝ちならそれぞれに3点、あいこのときは3人に2点ずつが与えられます。 計5回の勝負を行い、次のような結果になりました。
このとき、3人が出した延べ15回の手の内訳を考えて下さい。 |
2.解答例1(Tak'Sakaiさん、中村明海さん他多数)
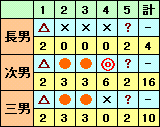
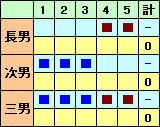
次男と三男の同じ手が3回あることから、残りの2回で次男が三男より6点多く得点するためには、下記のとおり、「次男の1人勝ちと3すくみ」、「長男と次男の2人勝ちが2回」の2ケースが考えられる。
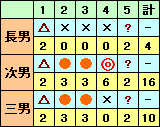
しかし、後者は長男の得点が4点を超えるので不適。前者のケースと分かる。
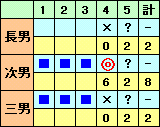
さて、長男の得点は4点なので1〜3までで2点取ることになるので、3人同じ手のあいこが1回、次男と三男の2人勝ち2回となる。
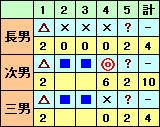
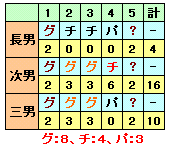
次男と三男が同じ手を出すのはグー、次男が勝つのは次男チー・三男パーのときしかないので、下図のように決まる。
5回目のさんすくみのあいこでは誰がどう出すかにかかわらず、グー、チョキ、パーがそれぞれ1回なので、結局グー8回、チョキ4回、パー3回となる。
答:グー8回、チョキ4回、パー3回以上
3.解答例2:得点に着目した場合
掲示板でのトラさんのコメントにもあるように、問題の条件が冗長になっています。
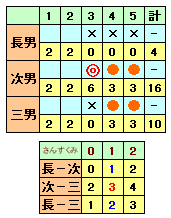
そこで、本題と同じ解1通りになるための最低限の条件を考えてみましょう。まず、得点は本題同様に次男16点、三男10点、従って長男は4点となるのであいこが2回あることになります。
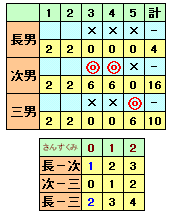
残り3回とも長男は負けとなりますが、次男が残り12点、三男が6点取るのは上図の2ケースのいずれかと考えられます。
また、あいこの2回のうち同じ手のあいことさんすくみのあいこの回数によってそれぞれ3ケースに分かれます。これらで、長男−次男、次男−三男、長男−三男の同じ手の回数は上図のとおりとなります。
従って、本題の解1通りに決まるためには、「次男−三男の同じ手が3回」とすればいいことになります。
以下、解1と同様。
4.解答例2:同じ手の回数に着目した場合
今度は、同じ手の回数が長男−次男1回、次男−三男3回、長男−三男2回としてみましょう。
まず、最初の3回は次男と三男が同じ手を出したとしましょう。
長男と三男が同じ手を出すのが、1〜3で2回、1〜3で1回・4〜5で1回、4〜5で2回の3ケースが考えられます。
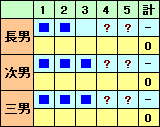
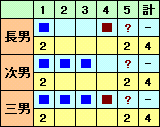
初めのケースでは、長男と次男が同じ手を2回出したことになり不適。
また、最後のケースでは、長男と次男が同じ手を1〜3で出したとすると、その回は三人が同じ手を出したことになり、長男と三男が2回に反します。
長男と次男が同じ手を4〜5で出したとすると、その回は三人が同じ手を出したことになり、次男と三男が3回に反します。結局、真ん中のケースとなります。
さて、4回目を除き次男と三男は各回とも同じ得点を取ることになるので、「次男の得点は三男より多い」とする必要があります。
従って、4回目は次男の1人勝ちとなります。2、3回目では「長男の1人勝ちが2回」、「長男の1人勝ち1回・次男と三男の2人勝ち」、「次男と三男の2人勝ち2回の3通りが考えられます。
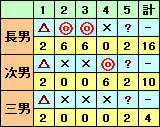
最後のケースが本題と同じ解ですので、このケースに絞られるためには、「三男の得点は長男より多い」としなくてはなりません。
結局、「得点は次男、三男、長男の順に多い」とすれば良いことになります。
以下、同様。