第９３問の解答

１．問題　［平面図形］

問題図

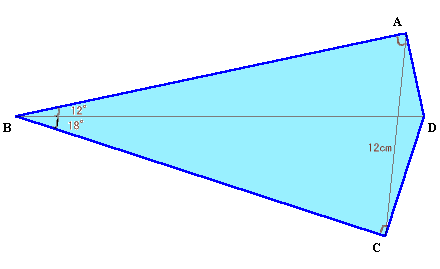
　上図のABCDはＡとCの角度が共に９０°の四角形です。
対角線ＡＣの長さが12cmのとき、もう一方の対角線BDは何cmでしょうか？

２．解答例１（佐藤彰夫さん、わかさひ君、小太りおじさん他多数）

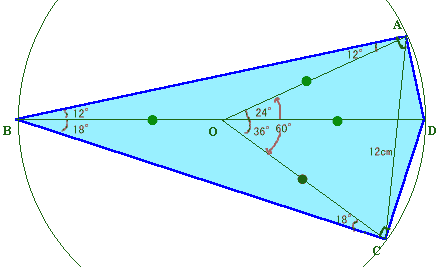
∠A、∠Cが直角なので、A、CはＢＤを直径とする円周上にある。
この円の中心、すなわちBDの中点をOとする。

参考図１

OA、OB、OC、ODは全て円Oの半径なので等しい。

すると、∠AOD＝∠OBA＋∠OAB＝２４°、∠COD＝∠OBC＋∠OCB＝３６°、
よって、∠AOC＝∠AOD＋∠COD＝６０°となります。

従って、△AOCは正三角形となるので、AC＝AO＝12cm、
よってBD＝OB＋OD＝２４ｃｍとなります。

答：２４ｃｍ

以上

３．解答例２（イデムリンさん、長野美光さん他）

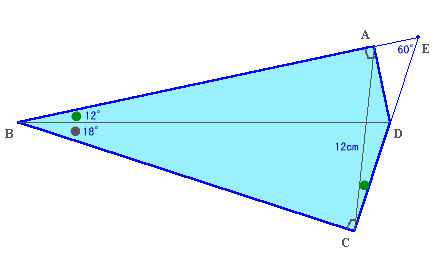
∠A、∠Cが直角なので、A、CはＢＤを直径とする円周上にある。
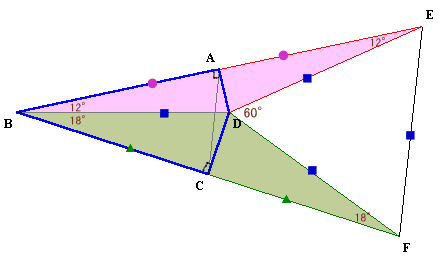
BAの延長線とCDの延長線の交点をEとする。

参考図２

△EBDとECAは、∠ACE＝∠ABD（円周角）、∠BED＝∠CEA＝６０°より相似。

△DAEは∠Eが６０°の直角三角形なので、ED：EA＝2：1。
よって、BD:AC＝２：１、故にＢＤ＝ＡＣ×２＝２４ｃｍと分かる。

４．解答例３（中学の数学コンさん、T.Endoさん他）

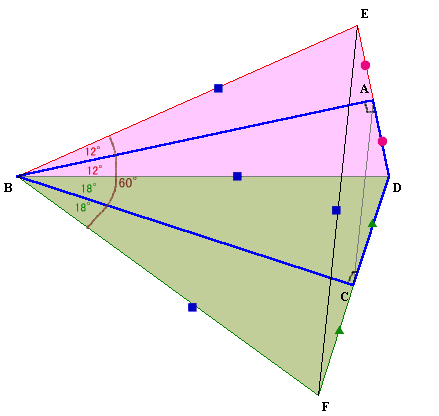
ABを軸に△ABDを折り返して△ＡＥＤ、ACを軸に△CBDを折り返して△CFＤとする。

参考図3

BE=BF=BD、∠EBF＝１２°×２＋１８°×２＝６０°より、△EBFは正三角形となる。
よって、EF=BD。

△DEFについて、中点連結定理より、EF=AC×２。

従って、BD=AC×２＝２４ｃｍ。

５．解答例４

ADを軸に△ABDを折り返して△ＡＥＤ、DCを軸に△CBDを折り返して△CFＤとする。

参考図４

DE=DF=BD、∠EDF＝１２°×２＋１８°×２＝６０°より、△EDFは正三角形となる。
よって、EF=BD。

△BEFについて、中点連結定理より、EF=AC×２。

従って、BD=AC×２＝２４ｃｍ。