第９４問の解答

---

１．問題　［規則性］

ある月の１日から３１日まで、毎日ＸとＹの２種類の製品を１個ずつ購入することになりました。以下は、この製品の値動きを記録したものです。 製品Ｘと製品Ｙの値段は、１日には同じでした。 その後Ｘは、毎日ａ円ずつ値上がりし、さらにある日を境にｂ円ずつ値を下げ、結局３１日には１日に比べて１５０円値上がりしました。 一方、製品Ｙは毎日ｃ円ずつ値下がりし、Ｘが最高値を付けた３日後に最安値を付けた後は、ｄ円ずつ値を上げ、結局３１日にはＸと同様に１５０円値上がりしていました。 　また、Ｘの最高値とＹの最安値の差は９００円でした。 この１ヶ月の間にＸを購入するのに要した代金の総額は、Ｙと比べていくら多かったのでしょう？

---

２．解答例１（DrKさん、長野美光さん、小太りおじさん他多数）

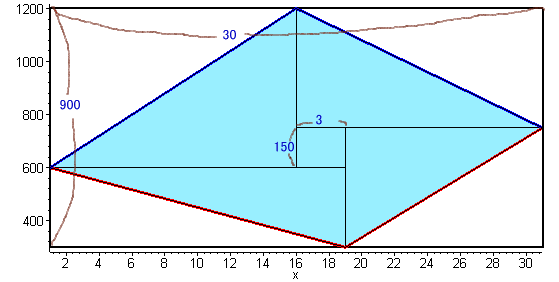
Ｘの購入費総額−Ｙの購入費総額＝Ｘの価格のグラフの面積−Ｙの価格のグラフの面積、すなわち下図青い部分の四角形の面積と考えることが出来る。（参考を参照）

外側の長方形の面積＝９００×３０から真ん中の長方形の面積＝１５０×３を除いたものが、求める面積から真ん中の長方形を引いた面積の２倍に等しい。

よって、求める面積＝（９００×３０−１５０×３）×１/２＋１５０×３＝１３７２５

従って購入費用総額の差は１３７２５円となります。

答：１３７２５円

以上

---

３．解答例２（sambaGREENさん、ｋｕｒｉ他）

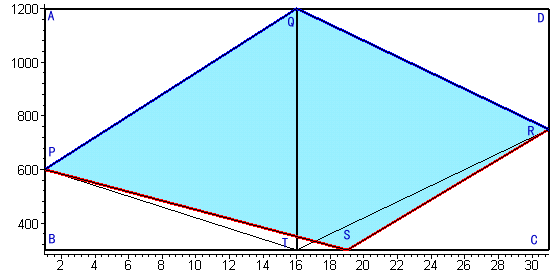
解答例１と同様、下図の四角形ＰＱＲＳの面積と考える。

　四角形ＰＱＲＳ
　　　＝５角形ＰＱＲＳＴ−△ＰＳＴ
　　　＝（四角形ＰＱＲＴ＋△ＲＳＴ）−△ＰＳＴ
　　　＝（長方形ABTQ×１/２＋長方形ＱＴＣＤ×１/２）＋（△ＲＳＴ−△ＰＳＴ）
　　　＝９００×３０×１/２＋１５０×３×１/２＝１３７２５円

　

（参考）面積で求められること

Ｘ、Ｙの毎日の価格をＸ１、Ｘ２、Ｘ３、・・・、Ｘ３１、Ｙ１、Ｙ２、Ｙ３、・・・、Ｙ３１とする。
また、Ｘはｎ日に最高値Ｘｎをとり、Ｙは、その３日後のｍ日に最安値をとるものとする。

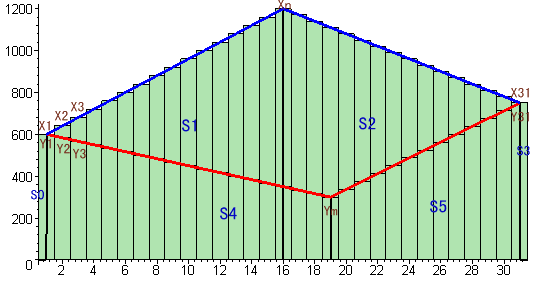
Ｘの費用計をｎ日の真ん中で２分して考えると、１日目のＸ１の半分Ｓ０、１日からｎ日までの面積Ｓ１、ｎ日から３１日の面積Ｓ２、３１日のＸ３１の半分Ｓ３の合計となることが分かる。
よって、Ｘの費用計＝Ｓ０＋Ｓ１＋Ｓ２＋Ｓ３。
同様に、Ｙの費用計＝Ｓ０＋Ｓ４＋Ｓ５＋Ｓ３

従って、Ｘの費用計−Ｙの費用計
　＝（Ｓ０＋Ｓ１＋Ｓ２＋Ｓ３）−（Ｓ０＋Ｓ４＋Ｓ５＋Ｓ３）
　＝（Ｓ１＋Ｓ２）−（Ｓ４＋Ｓ５）

---

４．解答例３

Ｘ１、Ｘ２、・・・ＸｎとＸｎ、Ｘn+1、・・Ｘ３１、およびＹ１、Ｙ２、・・・ＹｍとＹｍ、Ｙm+1、・・Ｙ３１は等差数列だから、

Ｘの費用計＝（Ｘ１＋Ｘ２＋・・＋Ｘｎ）＋（Ｘｎ＋Ｘn+1＋・・＋Ｘ３１）−Ｘｎ
　＝（Ｘ１＋Ｘｎ）×１/２×ｎ＋（Ｘｎ＋Ｘ３１）×１/２×（３２−ｎ）−Ｘｎ
　＝Ｘ１×１/２×ｎ＋Ｘｎ×１５＋Ｘ３１×１/２×（３２−ｎ）

Ｙの費用計＝（Ｙ１＋Ｙ２＋・・＋Ｙｍ）＋（Ｙｍ＋Ｙｍ+1＋・・＋Ｙ３１）−Ｙｍ
　＝（Ｙ１＋Ｙｍ）×１/２×ｍ＋（Ｙｍ＋Ｙ３１）×１/２×（３２−ｍ）−Ｙｍ
　＝Ｙ１×１/２×ｍ＋Ｙｍ×１５＋Ｙ３１×１/２×（３２−ｍ）

Ｘ１＝Ｙ１、Ｘ３１＝Ｘ３１より、
Ｘの費用計−Ｙの費用計
　＝　Ｘ１×１/２×（ｎ−ｍ）＋（Ｘｎ−Ｙｍ）×１５＋Ｘ３１×１/２×（ｍ−ｎ）
　＝（Ｘｎ−Ｙｍ）×１５＋（Ｘ３１−Ｘ１）×（ｍ−ｎ）
　＝９００×１５＋１５０×１/２×３＝１３７２５円

---