第９５問の解答

１．問題　［平面図形］

参考図１
　直経１０cmの円の内部に、同じ大きさの正方形のタイルを数枚、左図のように縦横まっすぐに並べました。
このとき使用したタイルの面積の総計は５８/９cm2でした。

さてこの場合、何枚のタイルを使ったのでしょうか？

　

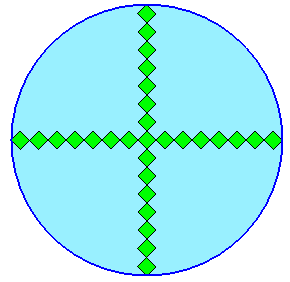２．解答例１（長野美光さん、わかさひ君、ヒデー王子他）

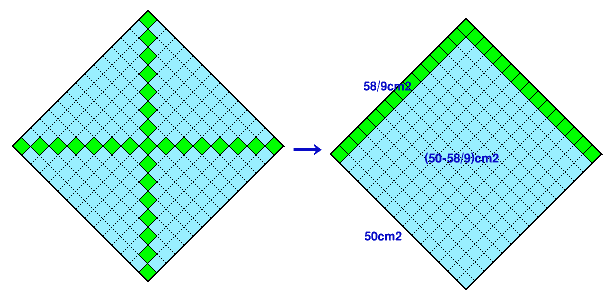
タイルを対角線の長さが10cmの正方形の端に集めると 、残りも正方形になります。

参考図１

大きい正方形の面積は、１０2/2＝５０cm2、小さい正方形は、（50-58/9)＝392/9cm2。
面積比は、５０：３９２/９＝２２５：１９６、よって相似比は√２２５：√１９６＝１５：１４。

よって，タイルは対角線上に15個並んでいる。全部では、15×2－1=29個となる。

答：２９個

以上

３．解答例２（むらかみさん他）

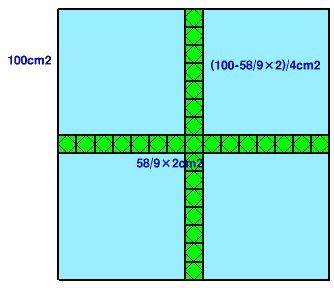
同じ数のタイルを加え、下図のように並べると、縦と横の長さが10㎝の十字になります。

参考図２

　タイルの面積は、５８/９×２＝１１６/９、
よって、４つある正方形の面積は、（１０×１０－１１６/９）／４＝１９６/９。
この正方形の１辺は、√１９６/９＝１４/３。

よって、小さい正方形の１辺は、１０－１４/３×２＝２/３cm。
縦に並ぶ正方形の数は、１０／（２/３）＝１５個。
全体では１５＋１４＝２９個。

従って、元のタイルも２９個あったことになる。

　

４．解答例３（杉本未来さん、ありさのお父さん、ＫＩＲＩさん他多数）

１列のタイルの数をｎとすると、１辺の長さは１０/ｎ、よって面積は （１０/ｎ）2／２ ｃｍ2。
タイルの数は、２×ｎ－１個あるので、面積は
　　（１０/ｎ）2／２×(２×ｎ－１)＝５８/９
　　(２×ｎ－１)／ｎ2＝２９/（９×５０） 。

これを解くと、ｎ＝１５、１５/２９を得るが、後者は不適。よって、ｎ＝１５個。

全体では、２×１５－１＝２９個となる