第97問の解答
1.問題 [整数の性質]
| 白石と黒石と小箱が何個かずつあります。 最初それぞれの小箱に白石と黒石の個数の比が5:9になるように石を入れていこうとしたところ、白石は3個余り、黒石は6個不足しました。 では、白石は何個あるのでしょうか? |
2.解答例1(杉本未来さん、YokoyaMacさん、CRYING DOLPHINさん他多数)
図1
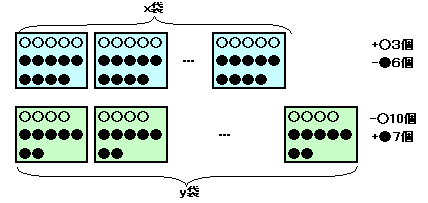
白石、黒石の個数をw、b個とする。また、最初白石5個と黒石9個を1袋にして合計x袋に入れたとし、あとは白石4個と黒石7個を1袋にして合計y袋に入れたものとする。
w=5x+3=4y−10 ・・・・ (1)
b=9x−6=7y+7 ・・・・ (2)
が成り立ちます。(1)、(2)より
−5x+4y=13 ・・・・ (3)
9x−7y=13 ・・・・ (4)(3)×7+(4)×4より、x=11×13=143
(3)×9+(4)×5より、y=14×13=182よって、w=5×143+3=718、b=9×143−6=1281
答:718個
以上
3.解答例2(ヒデー王子さん他)
図1より白石黒石全体で考えると、2通りの入れ方は共に3個不足するので、w+b+3は、5+9=14の倍数かつ4+7=11の倍数。14と11は互いに素だから14×11の倍数にもなる。従って、w+b+3=14×11×pとすると、x=11p、y=14pとなる。
大きな袋を用意して、白石5×11=55個、黒石9×11=99個をp袋に、白石4×14=56個、黒石7×14=98個をp袋に入ることになる。
図2
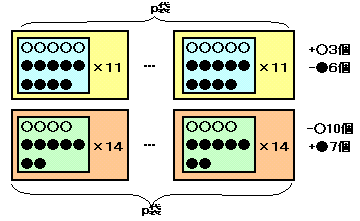
白石の合計数で見ると、後からのほうが56−55=1個ずつ多くなっており、この結果袋の外の白石が差し引き+3−(−10)=13個少なくなっている。
これから、p=13が得られ、w=5×11×13+3=718個と分かる。