第１００問の解答

---

１．問題　［規則性］

Ａ、B２つの水槽があって、Ａには１９９９ｄｌの水が入っていてＢは空になっています。 この水槽の水を次のように操作します。 Ａに入っている水の1/2をＢに移す。 Bに入っている水の1/3をAに移す。 Ａに入っている水の1/4をＢに移す。 Bに入っている水の1/5をAに移す。 　・・・　・・・ 最後にBに残っている水の1/1999をAに移したところで操作を終えました。 このとき、水槽Ａに入っている水の量は何dlでしょうか？

---

２．解答例１（多数）

全体の水の量を１とし、(k-1)回目の操作の結果水槽A、Ｂにある水の量A_k、B_kとします。
最初の４回の操作の結果は次の通り。

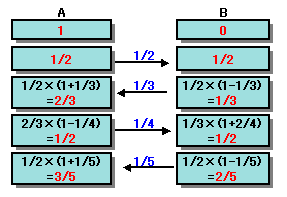
これから、次の結果が予想されます。

• 奇数回目：A_2m-2=1/2、B_2m-2=1/2。

• 偶数回目：A_2m-1=m/(2m-1)、B_2m-1=(m-1)/(2m-1)。

m=2のとき成り立つことは上図の通り。
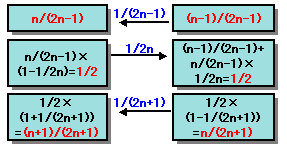
m=n(n≧2)のとき成り立つと仮定すると、

　A_2n=n/(2n-1)×(1-1/2n)
　　　=n/(2n-1)×(2n-1)/2n
　　　=1/2
　B_2n=(n-1)/(2n-1)+n/(2n-1)×1/2n
　　　=1/2
　A_2n+1=1/2×(1+1/(2n+1))
　　　　=1/2×(2n+2)/(2n+1)
　　　　=(n+1)/(2n+1)
　B_2n+1=1/2×(1-1/(2n+1))
　　　　=n/(2n+1)

よって、m=n+1のときも成り立つので、数学的帰納法により全てのmについて予想は成り立つことが分かります。

さて１９９８回目、k=2×1000-1のとき、A₁₉₉₉=1000/(2×1000-1)=1000/1999。

よって、Ａの水槽の水の量は、1999×1000/1999=1000dlとなります。

答：1000dl

以上

---