第１０１問の解答

---

１．問題　［石取りゲーム］

碁石がｎ個（ただしｎ≧１）あります。 　２人でこの碁石を交互に取っていくゲームをします。 　ルールは次の通りです。 最初からｎ個全ての碁石を取ることは出来ない。 必ず１個以上取らなくてはならない。 前の人が取った個数の２倍より多くの碁石は取れない。 最後の碁石を取ったほうが勝ち。 ２人は、それぞれ最善の手を尽くす。 このとき、後手必勝となるのはｎがいくつのときでしょうか？ ｎが小さい方から５つ答えて下さい。

---

２．解答例１

碁石の数がｎ個のとき、前の人が何個取ったか（ｍとします）によって条件が変わってきますので、それぞれ考える必要があります。

下表では、各（ｎ、ｍ）に対してＳは先手必勝、Ｇは後手必勝の場合を示しています。

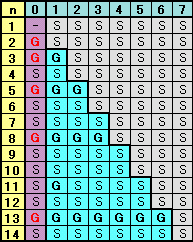
まず、すなわちｍ≧1のときを考えます。

• ｎ≦２ｍなら先手は全ての碁石を取ることが出来るので先手必勝。（上記灰色の部分）
  
  以下は、水色の部分を考えます。

• （ｎ、ｍ）＝（３、１）のとき：
  １個とれば（２、１）、２個とれば（１、２）の状態になるが、いづれも次の先手（すなわち後手）が必勝形なので、後手必勝。

• （ｎ、ｍ）＝（４、１）のとき：
  １個とれば（３、１）の後手（すなわち現在の先手）必勝状態になるので先手必勝。

• （ｎ、ｍ）＝（５、１）、（５、２）のとき：
  １個とれば（４、１）、２個とれば（３、２）、３個（（５、１）のときを除く）とれば（２、３）の状態になるが、いづれも次の先手必勝形なので、後手必勝。

• （ｎ、ｍ）＝（６、１）、（６、２）のとき：
  １個とれば（５、１）の後手必勝形になるので先手必勝。

• （ｎ、ｍ）＝（７、１）、（７、２）、（７、３）のとき：
  ２個とれば（５、２）の後手必勝形になるので先手必勝。

• （ｎ、ｍ）＝（８、１）、（８、２）、（８、３）のとき：
  次は（７、１）、（６、２）、（５、３）、（４、４）、（３、５）、（２、６）のいづれかの状態になるが、どれも先手必勝形になるので、後手必勝。

• （ｎ、ｍ）＝（９、１）、（９、２）、（９、３）、（９、４）のとき：
  １個とれば（８、１）の後手必勝形になるので先手必勝。

• （ｎ、ｍ）＝（１０、１）、（１０、２）、（１０、３）、（１０、４）のとき：
  ２個とれば（８、２）の後手必勝形になるので先手必勝。

• （ｎ、ｍ）＝（１１、２）、（１１、３）、（１１、４）、（１１、５）のとき：
  ３個とれば（８、３）の後手必勝形になるので先手必勝。
  （ｎ、ｍ）＝（１１、１）のとき：３個は取れないので、次は（１０、１）、（１０、２）のいづれかの状態になるが、どれも先手必勝形になるので、後手必勝。

• （ｎ、ｍ）＝（１２、１）、（１２、２）、・・・、（１２、５）のとき：
  １個とれば（１１、１）の後手必勝形になるので先手必勝。

• （ｎ、ｍ）＝（１３、１）、（１３、２）、・・・、（１３、６）のとき：
  次は（１２、１）、（１１、２）、（１０、３）、・・・、（１、１２）のいづれかの状態になるが、どれも先手必勝形になるので、後手必勝。

さて、ｍ＝０の場合（すなわちゲーム開始時の先手番：紫色の部分）を考えます。

• ｎ＝２、３、５、８、１３のとき：
  次の手は、どれも先手必勝形になるので、後手必勝。

• ｎ＝４、６、７、９、１０、１１、１２、１４のとき：
  次の手は、右上方向の対角線上にあるが、その中に後手必勝形が含まれるので先手必勝。

　

答：２、３、５、８、１３

以上

---