第１０２問の解答

１．問題　［平面図形］

問題図
　図のように、２枚の三角定規を使って四角形ＡＢＣＤを作りました。
このとき、対角線ＡＣの長さは１５ｃｍありました。

さて、四角形ＡＢＣＤの面積は何ｃｍ2でしょう？

　

　

２．解答例１（ヒデー王子さん他）

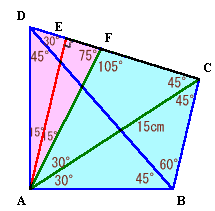
三角形ＡＢＣを切り取って辺ＡＢがＡＤと重なるように移します。

参考図1

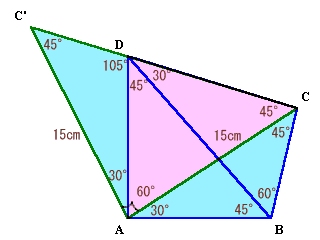
∠ＤＡＢ、∠ＢＣＤが直角であることから四角形ＡＢＣＤは円に内接することが分かります。

よって、円周角から
　∠ＡＣＢ＝∠ＡＤＢ＝４５度、
　∠ＣＡＢ＝∠ＣＤＢ＝３０度、
　∠ＤＡＣ＝∠ＤＢＣ＝６０度
となります。

すると、∠Ｃ'ＤＢ＝∠ＡＢＣ＝１０５度よりＣ'ＤＣは１直線上に並びます。

また、∠Ｃ'ＡＣ＝∠ＤＡＢ＝９０度、Ｃ'Ａ＝ＡＣ＝１５ｃｍから、
　四角形ＡＢＣＤの面積
＝直角２等辺三角形Ｃ'ＡＣの面積
＝１/２×１５2
＝１１２．５ｃｍ2

答：１１２．５ｃｍ2

以上

３．解答例２（サンデー毎日願望男さん他）

辺ＤＣ上にＥ、Ｆを∠ＥＡＣ＝４５度、∠ＦＡＣ＝３０度となるようにとります。

参考図2

すると、∠ＥＡＣ＝∠ＥＣＡ＝４５度より、∠ＡＥＣ＝９０度となり、△ＡＥＣは直角２等辺三角形となります。

また、∠ＤＦＣ＝∠ＦＡＣ＋∠ＤＣＡ＝７５度＝∠ＦＤＡ、よって△ＡＤＥ＝△ＡＦＥ。
∠ＣＡＦ＝∠ＣＡＢ＝３０度、∠ＡＣＦ＝∠ＡＣＢ＝４５度より△ＡＦＣ＝△ＡＢＣ。

よって、四角形ＡＢＣＤ＝△ＡＥＣ×２＝（１５/２）2×２＝１１２．５ｃｍ2。

４．解答例３（ぶぶおパパさん他）

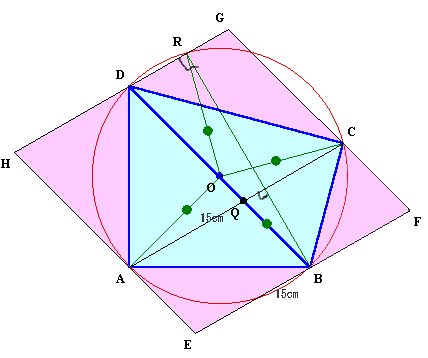
四角形ＡＢＣＤを４個並べると下図のように、対角線が３０ｃｍの正方形が出来ます。

参考図3

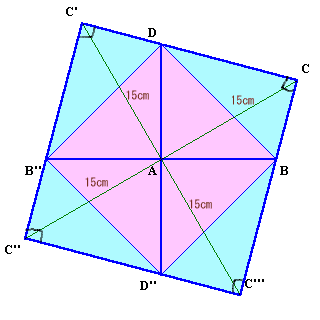
よって、四角形ＡＢＣＤ＝（１５2×２）×1/4＝１１２．５ｃｍ2。

５．解答例４（まさぴょんさん他）

Ａ、Ｃを通るようにＢＤに平行な直線ＥＨ、ＦＧを引き、Ｂ、Ｄを通るようにＡＣに平行な直線ＥＦ、ＨＧを引くと四角形ＥＦＧＨは平行四辺形となる。

参考図3

まず、ＥＦ＝ＡＣ＝１５ｃｍは明らか。
また、∠ＤＡＢ＝∠ＡＣＢ＝９０°だから、平行四辺形ＡＢＣＤは円Ｏに内接する。
従って、△ＯＡＣと△ＯＢＲは、どちらも円Ｏの半径を等辺とする２等辺三角形となる。

ところで、
∠ＯＡＣ＝∠ＯＡＢ−∠ＣＡＢ＝∠ＯＡＢ−∠ＢＤＣ＝４５°−３０°＝１５°、
∠ＯＢＲ＝９０°−∠ＣＱＢ＝９０°−（∠ＤＢＡ＋∠ＣＡＢ）
　　　　　＝９０°−（４５°＋３０°）＝１５°。

よって、底角が等しいので△ＯＡＣ＝△ＯＢＲ、
従って、ＲＢ＝ＡＣ＝１５ｃｍ。

 平行四辺形ＥＦＧＨ＝１５2＝２５５ｃｍ2。

四角形ＡＢＣＤ＝平行四辺形ＥＦＧＨ×1/2＝１１２．５ｃｍ2。