第１０３問の解答

---

１．問題　［平面図形］

左図のように、中心角が９０度の扇形OＡＢの円周部分に、これを３等分する点ＭとＮをとって、それぞれ結びました。 図の三角形ＯＰＱと三角形ＢNQの面積比は何：何でしょうか？

---

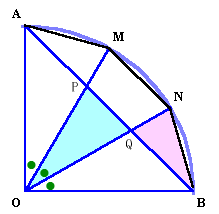２．解答例１（サンデー毎日願望男さん、南の源さん、長野　美光さん、CRYING DOLPHINさん、fumioさん他）

下図のように、△ＡＯＭ＝△ＡＭＮ＝△ＡＮＢと△ＯＰＱ、および△ＡＰＭ＝△ＮＢＱは相似な２等辺三角形となります。

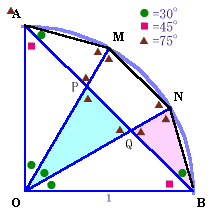
円の半径ＯＢ＝１とすると、ＮからＯＢへ下ろした垂線の長さ＝1/2となるので、
　△ＯＢＮ＝1/2×（１×1/2）＝1/4、
　△ＯＡＢ＝1/2×（１×1）＝1/2。

よって、四角形ＡＢＮＭ＝△ＯＢＮ×３−△ＯＡＢ＝1/4×３−1/2＝1/4。

従って、四角形ＡＢＮＭ＝△ＯＢＮ＝△ＯＭＮとなるので、共通部分である四角形ＰＱＮＭの面積を除くと、△ＯＰＱ＝△ＡＰＭ＋△ＢＮＱ＝△ＢＮＱ×２。

よって、△ＯＰＱ：△ＢＮＱ＝２：１となります。

答：２：１

以上

---

３．解答例２（ありさのお父さん、長野美光さん他）

△ＯＱＢについて正弦定理より、ＯＱ／ｓｉｎ４５°＝ＢＱ／ｓｉｎ３０°。

よって、ＯＱ：ＢＱ＝ｓｉｎ４５°：　ｓｉｎ３０°＝√2/2　：1/2＝√２：１。

△ＯＰＱと△ＢＮＱは相似なので面積は、辺の２乗に比例。

△ＯＰＱ：△ＢＮＱ＝ＯＱ²：ＢＱ²＝２：１。

---