第１０５問の解答

---

１．問題　［場合の数］

円形の板を左図のように６つの部分に等分します。 この６個所を赤、黄、青、黒の４色を全て使って塗り分けます。 （隣り合う場所に同じ色は使いません）　 円板を回転したとき同じになるものは１種類と考えることにすると、 塗り分け方は全部で何通りあるでしょうか？

---

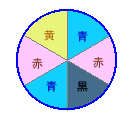２．解答例１（杉本未来さん、小太りおじさん、ぱぱりんさん、Hamayanさん、中村明海さん他多数）

色塗りのパターンで場合分けします。
６個所のうち４個所を異なる４色塗ったとして、あと２個所は既に使った４色のいづれかを使用する必要があります。
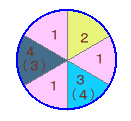
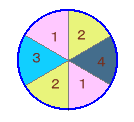
以下では、色を１，２，３，４の番号で表すことにします。

（１）３個所を同一色で塗る場合（残り２個所を同じ色で塗る）

・１の色を選ぶのに４通り、 あとは、残り３個所を右回りに ２，３，４または２，４，３の２通り の塗り方があるので、 　計４×２＝８通り

（２）２個所ずつを同一色で塗る場合（残り２個所を異なる色で塗る）

残り２個所の配置で場合分けします。

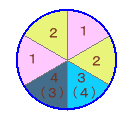
・残り２個所が隣り合う場合

１，２，３の個所に４色から３色選べば 残り１色は自動的に決まるので 　４×３×２＝２４通り

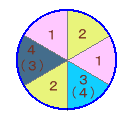
・残り２個所が１個おいた隣にくる場合

１，２，３の個所に４色から３色選べば 残り１色は自動的に決まるので 　４×３×２＝２４通り

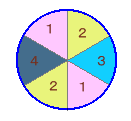
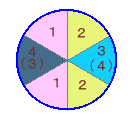
・残り２個所が対角線にくる場合

　同じ色を２個所に使う色の配置が、１，２，１，２の場合と１，２，２，１の２通りに分かれます

（１，２，１，２の場合）

１，２の２個所に４色から２色選べば 残り２色はどう並べても同じになるので、 　４×３＝１２通り

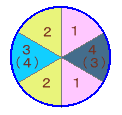
（１，２，２，１の場合）

１，２，３の３個所に４色から３色選べば 残り１色は自動的に決まるが、左の２例 のように回転すると同一になるものを重複 して数えているので、 　（４×３×２）／２＝１２通り

よって、合計８＋２４＋２４＋１２＋１２＝８０通りとなります。

答：８０通り

以上

---