第106問の解答
1.問題 [平面図形]
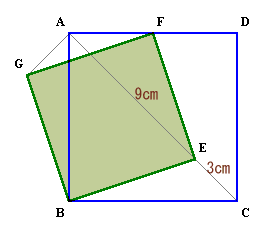 |
|
2.解答例1(加藤瑛美さん、ありさのお父さん他)
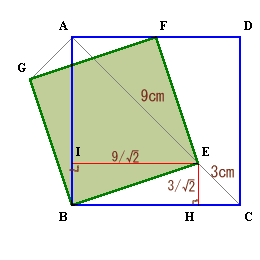
Eから辺BCに下ろした垂線の足をH、
辺ABに下ろした垂線の足をIとする。EC=3cmだからEH=3/√2cm、
AE=9cmだからEI=9/√2cm。よって、
正方形BEFGの面積
=BE2
=EH2+EI2
=9/2+81/2
=45cm2答:45cm2
以上
3.解答例2(杉本未来さん他)
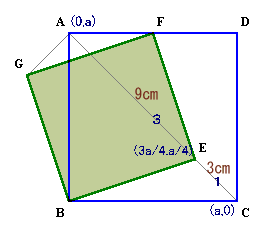
Bを原点、BCをx軸、ABにをy軸とする座標軸で考える。
AB=BC=aとすると、
A=(0,a)、B=(a,0)となる。EはACを3:1に内分する点だから、
E=1/4×A+3/4×C
=(3a/4,a/4)よって、正方形BEFGの面積
=BE2
=(3a/4)2+(a/4)2
=5/8×a2
=5/8×(122×1/2)
=45cm2
4.解答例3(おりくん他)
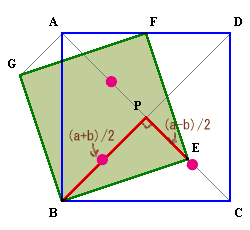
対角線AC、BDの交点をP、
AE=a、EC=bとする。
AP=AC/2=(a+b)/2
PE=PC-EC=(a+b)/2-b
=(a-b)/2よって、正方形BEFGの面積
=BE2
=((a+b)/2)2+((a-b)/2)2
=(a2+b2)/2
=(92+32)/2
=45cm2
5.解答例4(まさぴょん他)
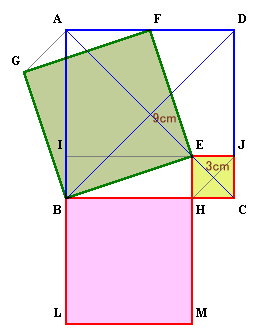
左図のように、正方形BLMH、EHCJを作ると、BH:HC=AE:EC=3:1。 正方形BEFGの面積をSとすると、
S=122/2=72cm2。ピタゴラスの定理より、
正方形BEFGの面積
=BLMHの面積+EHCJの面積
=(3/4)2×S+(1/4)2×S
=5/8×S
=5/8×72
=45cm2
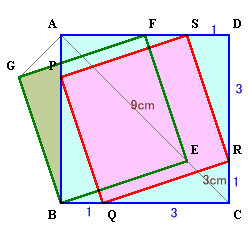
6.解答例5(長野美光さん他)
正方形BEFGを頂点Eが辺CD上にくるまで、右方向に移動する。
CR:RD=EC:AE=1:3。BQ=ER=1/4×BCより、
BQ:QC=1:3。
よって、△QCRと△RDSは合同。GB=BE、BA=BC、角GBA=角EBCより、△AGBと△CEBは合同。
よって、
GP=EからBCへ下ろした垂線の高さ
=RC=ER
従って、Pは辺AB上にあることなり、
結局正方形PQRSは、ABCDに内接する。従って、△PBQ、△SAPも△QCRと合同。
ABCDの面積=Sとすると、
正方形BEFGの面積
=S−△QCRの面積×4
={1−(3/4)×(1/4)×1/2×4}×S
=5/8×S
=5/8×72
=45cm2
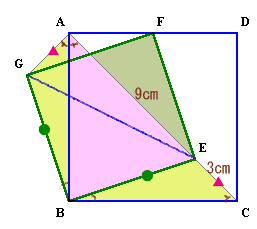
7.解答例6(ヒデー王子さん他)
解答例5と同様にして、△AGBと△CEBは合同。 よって、四角形AGBEの面積
=△ABE+△AGB
=△ABE+△CEB
=△ABC
=36cm2。また、AG=CE=3cm、
角EAG=角BAG+角EAB
=45+45=90°。よって、
△EAG=1/2×3×9=27/2cm2。従って、
△EGB=四角形AGBE−△EAG
=36−27/2
=45/2cm2。よって、
正方形BEFGの面積
=△EGB×2
=45cm2
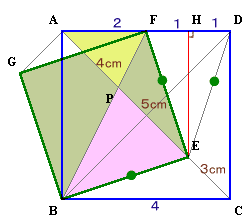
8.解答例7(エウロパさん他)
Eより辺ADに垂線EHを下ろす。
AH:HD=AE:EC=3:1。また、ED=BE=EFより、
三角形EDFは、2等辺三角形となり、
FH=HD。よって、AF:FH:HD=2:1:1。
また、△APFと△CPBは相似で、、
相似比はBC:AF=2:1。よって、AP=AC×1/3=4cm、
PE=AE−AP=5cm。従って、
△PBE=△ABC×5/12
=36×5/12
=15cm2。よって、
△BEF=△PBE×3/2=45/2cm2。正方形BEFGの面積
=△BEF×2
=45cm2