第１０７問の解答

１．問題　［空間図形］

問題図
１辺が１０cmの立方体の中に直径１０cmの球を入れてあります。

A、B、Cの３点を通る平面でこれを切断したとき、球の切断面の面積は何ｃｍ2になるでしょうか？　円周率＝3.14として求めて下さい。

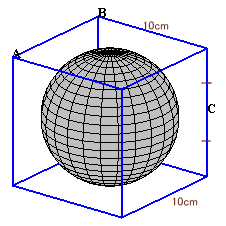２．解答例１（ありさのお父さん他多数）

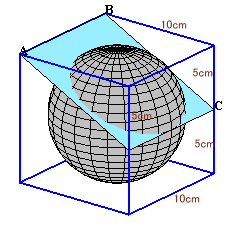
３点A,B,Cを通る平面は、下図のようになるので、球の切断面は円となり、その直径は図２の円（球）を切断する線分、すなわち図３のＣ'Cとなります。

図１
参考図1		 図２
参考図2
図３
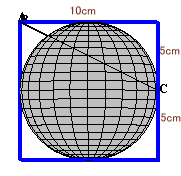
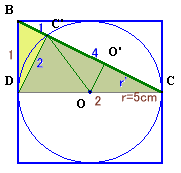
参考図3
△ＢＤＣと△ＢＣ'Ｄ、△ＤＣ'Ｃは、
それぞれ２辺の比が１：２の相似な直角三角形となる。

よって、ＢＣ'：Ｃ'Ｄ＝１：２、Ｃ'Ｄ：Ｃ'Ｃ＝１：２、
ＢＣ'：Ｃ'Ｃ＝１：４となる。
これから、△ＢＤＣ：△ＤＣ'Ｃ＝５：４と分かる。

ＤＣを直径とする円Ｏの半径をｒ、面積をＳ、
Ｃ'Ｃを直径とする円Ｏ'の半径をｒ'、面積をＳ'とする。
　Ｓ：Ｓ'＝πｒ2：πｒ'2＝ｒ2：ｒ'2。

ところで、
　△ＢＤＣ＝1/2×ｒ×２ｒ＝ｒ2、
　△ＤＣ'Ｃ＝1/2×ｒ'×２ｒ'＝ｒ'2
よって、ｒ2：ｒ'2＝５：４、
　Ｓ'＝Ｓ×4/5
　　＝π×５2×4/5
　　＝3.14×２０
　　＝62.8ｃｍ2

以上

（別解）
　ＢＣ＝√（ＢＤ2＋ＣＤ2）＝５√５ｃｍ。
　Ｏ'Ｃ＝ＯＣ×ＣＤ/ＢＣ＝５×１０/５√５＝２√５ｃｍ。
　Ｓ'＝3.14×(２√５)2＝3.14×２０＝62.8ｃｍ2