第１０９問の解答

１．問題　［場合の数・最短経路］

　

ＡチームとＢチームが４戦先取の７回戦試合をすることになりました。
１回戦はＡチームが勝ちました。（試合はどちらかのチームが４勝した時点で打ち切ります）

では、残りの試合結果は何通りあると考えられるでしょうか？

２．解答例１（杉本未来さん他多数）

参考図1

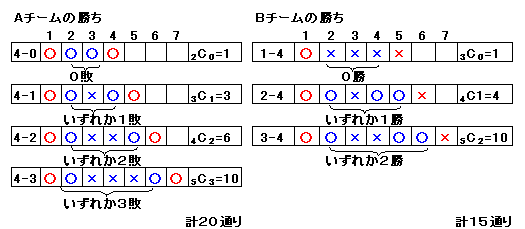
Ａチームが勝つ場合は、計２０通り、Ｂチームが勝つ場合は計１５通り、
合計３５通りとなる。

以上

３．解答例２（ありさのお父さん、杉本未来さん他多数）

どちらかが４勝して勝敗が決着しても、残り試合を他方が勝つことにして考える。

参考図2

上図のようにして、Ａチームの勝２０通り、Ｂチームの勝１５通り、合計３５通りとなる。

４．解答例３（sambaGREENさん、中村明海さん、 中学への算数学コンさん、 航介さん他多数）

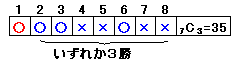
どちらかが４勝して勝敗が決着しても、残り試合を他方が勝つことにして８試合行うものと考えると、下図のように７試合中Ａチームが３勝すればいいので、3+4C3＝３５通りとなる。

参考図4

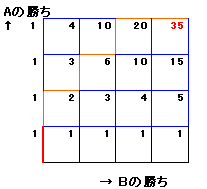
これは、３×４の最短経路として考えると、下図のようにＡの１勝を上へ進む、Ｂの１勝を右へ進むことにすれば、3+4C3＝３５通りとなる。

参考図3

あるいは、Ａが１勝した時点から格子点ごとに場合の数を加えていけば、合計３５通りと数え上げることが出来る。