第１１０問の解答

---

１．問題　［平面図形］

図１

図２

正方形の折り紙が１枚あります。 これを図１のように、対角線と平行な折り目を付けて折り返し、２枚重ねになっている部分の面積を求めます。 次に、図１の左側を折り返し、図２のような状態にしました。 このとき、２枚重ねになっている部分の面積は、図１のときと比べて６３ｃｍ2減っていました。 また、枚数が重なっている部分の面積比は、４枚重ね：３枚重ね：２枚重ね＝１：２：９になっていました。 さて、元の正方形の面積は何ｃｍ2だったでしょうか。

---

２．解答例１（ありさのお父さん、CRYING DOLPHINさん、長野美光さん他多数）

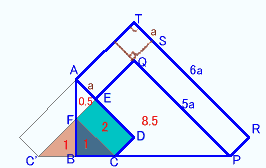
２枚重ね、３枚重ね、４枚重ねの部分は図３のようになり、それぞれの面積をＳ２、Ｓ３、Ｓ４とすると、Ｓ ４：Ｓ３：Ｓ２＝１：２：９である。
ただし、２枚重ねは２個所に分かれるので、小さい方をＳ２'、大きい方をＳ２''とする。

図３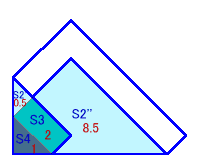

図４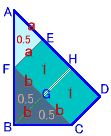

Ｓ２'＝Ｓ４×０．５が次のようにして分かる。
図４のように点、辺の長さをとると、
　△ＦＢＧ＝1/2ｂ²＝Ｓ４×０．５、四角形ＥＦＧＨ＝ａｂ＝Ｓ４。
よって、1/2ｂ²：ａｂ＝１：２、従ってａ＝ｂとなる。
よって、Ｓ２'＝△ＡＦＥ＝1/2ａ²＝Ｓ４×０．５

これより、Ｓ２''＝Ｓ２−Ｓ２'＝Ｓ４×８．５。

上図のように、図１の２枚重ねと図２の２枚重ねの面積差は、
　４角形Ｃ'ＣＤＥ−△ＡＦＥ＝Ｓ４×４−Ｓ４×０．５＝６３ｃｍ²。

よって、Ｓ４＝６３／３．５＝１８ｃｍ²。

さて、△Ｃ'ＰＱ＝Ｓ４×１２．５＝1/2×（５ａ）²。

よってＳＲ＝ＰＱ＝５ａ。
ＴＳ＝ＡＥ＝ａだから、もとの正方形の１辺ＴＲ＝６ａ。
したがって、求める正方形の面積＝（６ａ）²＝３６ａ²＝３６×１８＝６４８ｃｍ²。

答：６４８ｃｍ²

以上

---