第１１１問の解答

１．問題　［速さ］

　幅の広い下りのエスカレータがあります。Ａ君、Ｂ君の２人が、各々のペースでこのエスカレータを９分間上り下りし続けます。このとき、Ａ君が下る速さとＢ君が上る速さは、等しかったそうです。

  • Ａ君は、下の階を出発し、２往復してちょうど下の階に戻ってきました。

  • Ｂ君は、上の階を出発し、２往復半してちょうど下の階に着きました。

  • 途中、２人が２回目にすれ違ったのは、スタートして３分５秒後で、下から５１段目の場所でした。

　では、２人が最後にすれ違ったのは、下から何段目の場所でしょう？

問題図

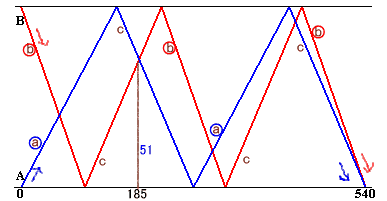
２．解答例１（gehoさん他）

Ａ君の上り速度をａ段/秒、Ｂ君の下り速度をb段/秒、Ａ君の下り速度およびＢ君の上り速度をb段/秒とします。

Ａ君は上り（ａ段/秒）と下り（ｃ段/秒）を２回ずつ、Ｂ君は上り（ｃ段/秒）2回、下り（ｂ段/秒）3回ですから、ａ：ｂ＝２：３と分かります。

参考図1

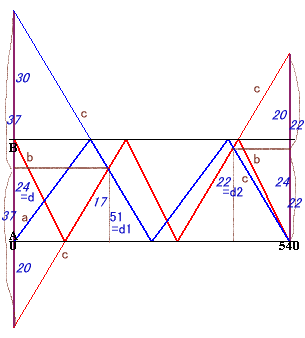
また、Ａ君、Ｂ君、およびエスカレータ自身の速度をそれぞれva,vb,ｖ段/秒とすると、
　　a=va-v,b=vb+v,c=va+v=vb-v
よって、a=ｃ-2v,b=c+2vとなり、ｃは、ａとｂの平均となる。
従って、ａ：ｃ：ｂ＝２：２．５：３＝４：５：６と分かります。

エスカレータの段数、２回目に出会った場所を下から数えた段数、最後に出会った場所の段数をｄ、ｄ１、ｄ２段とする。今、ｄを２４とすると、

Ａ君が上りもｃ段/秒で上ったとすると、ｄ×ｃ/ａ＝３０段上る、
Ｂ君が下りもｃ段/秒で下ったとすると、ｄ×ｃ/ｂ＝２０段下ることになります。

従って、２人で合計３０＋２４＋２０＝７４段進んだことになるので、１人では半分の３７段になります。

よって、ｄ：ｄ１＝２４：（３７−２０）、ｄ１＝５１だからｄ＝５１×２４/１７＝７２段になります。

今度は、２人が最後に出会ってから以降を考えると、同様にして２人で２４＋２０＝４４段、１人では４４/２＝２２段進んだことになります。

よって、ｄ：ｄ２＝２４：２２、ｄ２＝７２×２２/２４＝６６段と分かります。

答：６６段

以上

３．解答例２（ありさのお父さん、中学への算数学コンさん他）

下図のように、２人が出会う時間をｔ１，ｔ２秒、Ａ君が各階に着く時間をta1,ta2,ta3秒、Ｂ君が各階に着く時間をtb1,tb2,tb3,tb4秒とします。

参考図2

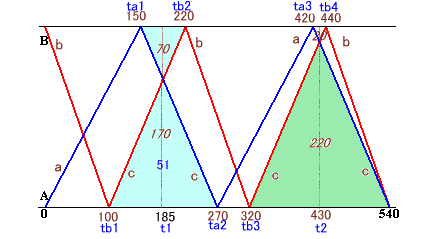
まず、Ａ君は、上り下り２回ずつなので、ta2=540/2=270秒となります。

Ｂ君がtb1からt1までと、Ａ君がt1からta2までと、どちらも同じ速度ｃで進むので、tb1,t1,ta2は等間隔。よって、tb1=185×2-270=100秒となります。

すると、Ｂ君が下るのには１００秒かかることになり、tb4=540-100=440秒、tb2=tb4/2=220秒、tb3=tb2+100=320と分かります。

これからＢ君が上りに要する時間は、tb2-tb1=１２０秒となります。
すると、Ａ君が上りに要する時間は、ta3-ta2=420-270=150秒と分かります。
よって、ta1=150となります。

さて、１階から２人が２回目に出会うまでの５１段を、往復２７０−１００＝１７０秒要し、出会う場所から２階までの往復に２２０−１５０＝７０秒要する。

よって、ｄ＝５１×（７０＋１７０）/１７０＝５１×２４/１７＝７２段、
　　ｄ２＝７２×２２０/（２０＋２２０）＝７２×２２/２４＝６６段となります。

以上