第１１３問の解答

１．問題　［空間図形］

問題図

　左図で、中央の四角形は面積が７２cm2ある正方形、その回りは正三角形です。

　これを組み立てたときにできる立体の体積は何cm3あるでしょうか？

　

２．解答例１（CRYING DOLPHINさん、長野美光さん、わかさひ君、sambaGREENさん、gehoさん他）

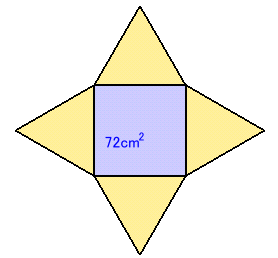
正方形の対角線を１辺とする正方形の面積は、７２×２＝１４４cm2になります。
従って、対角線の長さは１２ｃｍと分かります。

求める四角錐の斜辺の長さは、底面である正方形の１辺と等しい。
よって、求める四角錐は、正八面体の半分ＯＰＱＲＳになります。

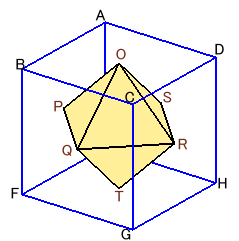
図１（俯瞰図）
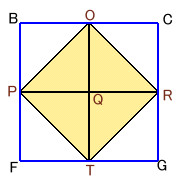
参考図1		 図２（正面から見た図）
参考図2
（参考）マウスでドラッグして下さい。

図１、図２のように立方体の各面の中心を結んで出来る立体は正八面体となるので、求める四角錐の高さは、ＯＨの半分＝１２／２＝６ｃｍとなります。

よって、体積は1/3×７２×６＝１４４ｃｍ3となります。

答：１４４cm3

以上

３．解答例２（杉本未来さん、大西俊郎さん、ありさのお父さん他）

参考図3

正方形の１辺の長さをaとすると、a2＝７２より、a＝６√２ｃｍ2となります。

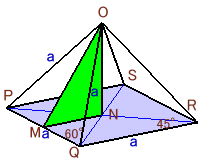
ＭをＰＱの中点、ＮをＰＱＲＳの重心とすると、ＯＭ＝√３/２ａ、ＭＮ＝１/２aとなるので、
ＯＮ2＝ＯＭ2−ＭＮ2＝３/４ａ2−１/４ａ2＝1/２ａ2＝1/２ａ2、
ＯＮ＝１/√２ａ＝６ｃｍと分かります。

よって、求める体積は、1/3×７２×６＝１４４ｃｍ3となります。