第115問の解答
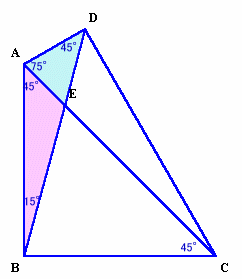
1.問題 [平面図形]
 |
|
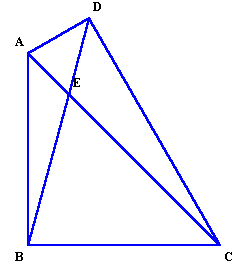
2.解答例1(sambaGREENさん、長野美光さん、ありさのお父さん他)
角ABCと角ADCは、ともに直角だからABCDは同一円周上にある。
円の中心をOとすると、AO、BO、CO、DOは全て円の半径rに等しい。
図1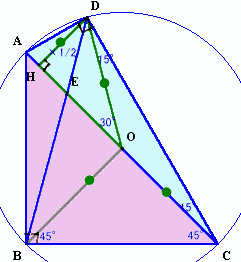 |
図2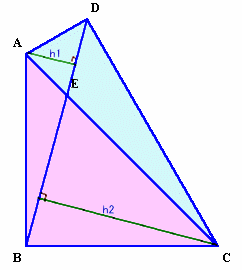 |
さて、DからACに下ろした垂線の足をHとする。
角DCA=角ABD=15°(円周角)、角ODC=角OCD=15°(2等辺三角形)
よって、角AOD=角ODC+角OCD=30°となり、三角形ODHは角度が30、60、90°の直角三角形になる。
従って、DH=r×1/2と分かります。
△ACD=1/2×AC×DH、△ABC=1/2×AC×BO、
よって、△ACD:△ABC=DH:BO=1:2。また、図2のように考えると、
△ACD=1/2×DE×h1+1/2×DE×h2=1/2×DE×(h1+h2)、
△ACB=1/2×EB×h1+1/2×EB×h2=1/2×EB×(h1+h2)、
よって、△ACD:△ABC=DE:EB=1:2。答:1:2
以上
3.解答例2(ヒデー王子さん、たなかさん他)
ABCDの外接円の中心OからDBへ下ろした垂線の足をGとする。
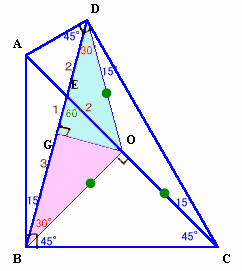
OD=OB、角ODG=角OBG=30°、よって、DG=BG。
角OEG=180−(角EBO+角BOE)=180−(30+90)=60°、
よって、EG:EO=1:2。ここで、EG=1とすると、EO=2。また、EO:EB=1:2より、EB=4。
GB=EB−EG=3、
DE=DG−EG=GB−EG=3−1=2。よって、DE:EB=2:4=1:2。
4.解答例3(むらかみさん他)
CDを軸にして三角形ADCを折り返し、三角形A'DCを作り、A'からACへ下ろした垂線の足をHとする。
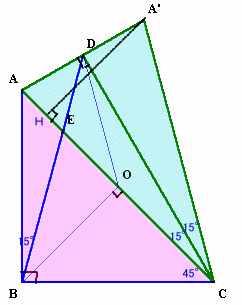
角A'CH=角ACD+角A'CD=15+15=30°。
よって、A'CHは、角度が30、60、90°の直角三角形となり、
A'H=A'C×1/2=AC×1/2。また、ABCは、2等辺直角三角形なので、BO=AC×1/2。
△A'AC=1/2×AC×A'H、△ABC=1/2×AC×BO、
よって△A'AC=△ABC。△DAC=1/2×△A'AC=1/2×△ABC。
以下、解答例1と同じ。
5.解答例4(kuri他)
ACを軸にして三角形ADCを折り返し、三角形AFCを作る。
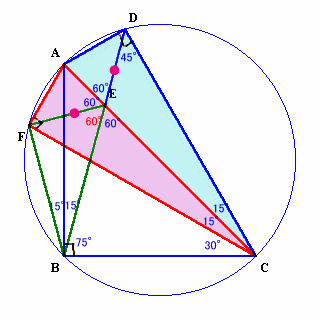
角ADC=角AFC=角ABC=直角より、ABCDおよびFは同一円周上にある。
対象性より、DE=FE、角AEF=角AED。
角AEF=角AED=角EDC+角DCE=45+15=60°。
角BEC=角AED=60°。
よって、角FEB=180−(角AEF+角BEC)=180−(60+60)=60°。また、角FBE=角FCD=30°(円周角)。
従って、三角形EFBは、角度が30、60、90°の直角三角形になり、
FE:EB=1:2、よってDE:EB=1:2。