第１１６問の解答

１．問題　［場合の数・規則性］

問題図

　左図のような縦３行×横４列のマス目があります。
このマス目を赤色と青色の２色で塗ります。
ただし、赤色はとなり同士で並べて塗ることはできません。

塗り方は何通りあるか求めて下さい？（全て青色も可）

２．解答例１（ヒデー王子さん、CRYING DOLPHINさん、あだっちさん、きょえぴさん、ありさのお父さん他）

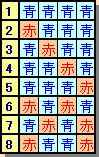
横１行４個のマス目のときを考えると、塗り方は下図のように８通りあります。

参考図1

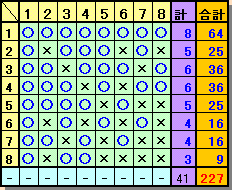
それぞれのパターンに対して、上隣または下隣に置くことのできるパターンを調べると下図のように、８、５、６、６、５、４、４、３通り（計の欄）になります。

参考図2

従って、塗り方合計は、
　８2＋５2＋６2＋６2＋５2＋４2＋４2＋３2＝２２７通りとなります。

答：２２７通り

以上

３．解答例２（伊藤　大輔さん他）

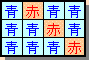
縦１列３個のマス目のときを考えると、塗り方は下図のように５通りあります。

参考図3

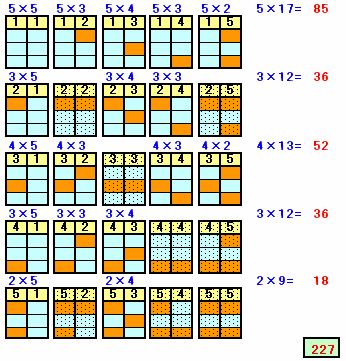
隣り合う２列に、上記パターンを配置できる組み合わせを調べると下図のようになる。

参考図4

真ん中の２列に、上記パターンを配置し、左側と右側に置けるパターン数をそれぞれ計算すると、
　５×１７＋３×１２＋４×１３＋３×１２＋２×９＝２２７通りとなる。

　

４．解答例３（たなかさん他）

列数ｎに関する数列で考える。
右端の列が解答例２のパターン１、２、３、４、５になるときの場合の数を、a(n)、b(n)、c(n)、d(n)、e(n)とする。

　a(n)＝１、b(n)＝１、c(n)＝１、d(n)＝１、e(n)＝１　および
　a(n)=a(n-1)+b(n-1)+c(n-1)+d(n-1)+e(n-1) 
　b(n)=a(n-1)　　　　+c(n-1)+d(n-1) 
　c(n)=a(n-1)+b(n-1)　　　　+d(n-1) +e(n-1)
　d(n)=a(n-1)+b(n-1)+c(n-1) 
　e(n)=a(n-1)　　　　+c(n-1)
が成り立つので、n=２、３、４と順次求めていくと下図のように、
a(n)＝63、b(n)＝42、c(n)＝50、d(n)＝42、e(n)＝30が得られる。

参考図5


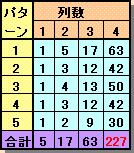
従って、合計＝６３＋４２＋５０＋４２＋５０＝２２７通りとなる。

（参考）（あれふさん、清川育男さん他）

１行n列の場合は、フィボナッチ数列になることが次のように示すことが出来ます。 
右端が青の場合をa(n)、赤の場合をb(n)とすると、
　a(1)=1、b(1)=1、
　a(n)=a(n-1)+b(n-1)　・・・　（１）
　b(n)=a(n-1)　　　　　・・・　（２）

（２）より、b(n-1)=a(n-2)となり、（１）に代入して、
　a(n)=a(n-1)+a(n-2)　が得られます。

一般式は、a(n)=(5+3√5))/10・αn-1+(5-3√(5))/10・βn-1（ただし、α=(1+√5)/2、β=(1-√5)/2）
と表せますので、求める場合の数は、a(n+1)=(5+3√5))/10・αn+(5-3√5)/10・βnとなります。

　

２行n列の場合、右端が青・青の場合をa(n)、赤・青の場合をb(n)、青・赤の場合をc(n)とすると、
　a(1)=1、b(1)=1、c(1)=1、
　a(n)=a(n-1)+b(n-1)+c(n-1)　・・・　（３）
　b(n)=a(n-1)　　　　+c(n-1)　・・・　（４）
　c(n)=a(n-1)+b(n-1)　　　　　・・・　（５）
となります。

（５）より、c(n-1)=a(n-2)+b(n-2)なので、（３）、（４）に代入して、
　a(n)=a(n-1)+a(n-2)+b(n-1)+b(n-2)　・・・　（６）
　b(n)=a(n-1)+a(n-2)　　　　+b(n-2)　・・・　（７）
となります。

（６）−（７）より、
　a(n)-b(n)=b(n-1)、よってa(n)=b(n)+b(n-1)、b(n-1)+b(n-2)=a(n-1)となる。
（６）に代入して、
　a(n)=2a(n-1)+a(n-2)を得る。　

一般式は、a(n)=(1+√2))/2・αn-1+(1-√2)/2・βn-1（ただし、α=1+√2、β=1-√2）
と表せますので、求める場合の数は、a(n+1)=(1+√2))/2・αn+(1-√2)/2・βnとなります。

３行n列、４行n列の場合、漸化式は、
　a(n)=2a(n-1)+6a(n-2)-a(n-4)
　a(n)=2a(n-1)+18a(n-2)+9a(n-3)-23a(n-4)-2a(n-5)+6a(n-6)-a(n-7)　
となるようです。

なお、４行４列のとき、場合の数は１２３４になります。