第１１７問の解答

１．問題　［平面図形］

問題図

　左図のようなＡＤ＝ＢＣ＝３５ｃｍの平行四辺形があります。
　点Ｐは、Ａを出発して毎秒１ｃｍの速さでＤまで動きます。
　点ＱはＣをＰと同時に出発して毎秒６ｃｍの速さでＣＢ間を３往復します。
　出発後、四角形ＡＢＱＰの面積が平行四辺形ＡＢＣＤの半分になるのは、出発から何秒後になるでしょう？

答が複数あるときは、全てを求めて下さい。

２．解答例１（たなかさん、ありっちさん、有無相生さん他）

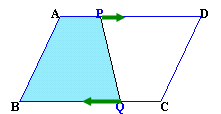
ＡＢＱＰの面積が平行四辺形ＡＢＣＤの半分になるのは、ＡＰ＝ＣＱとなるときである。

参考図1

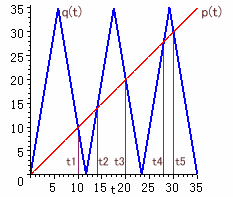
従って、p(t)＝ＡＰ、q(t)＝ＣＱとすると、ｙ＝p(t)、ｙ＝q(t)のグラフの交点を求めれば良いことになる。上図から、５つの答（t1、t2、・・・t5）があることが分かる。

（１）t1
　Ｑの動く速さはＰの６倍であることから、t=0〜t1間でQが進む距離は、同じ時間にＰが進む距離ｔ１の６倍。また、t=t1〜35/3にQが動く距離もｔ１である。
　よって、ｔ１×（６＋１）＝２×３５、ｔ１＝３５×２/７＝１０秒後。

参考図2

（２）t２
　Ｑの動く速さはＰの６倍であることから、t=0〜t２間でQが進む距離は、同じ時間にＰが進む距離ｔ2の６倍。また、t=35/3〜ｔ２にQが動く距離もｔ２である。
　よって、ｔ2×（６−１）＝２×３５、ｔ2＝３５×２/５＝１４秒後。

参考図3

（３）t３
　t=0〜t3間でQが進む距離は、同じ時間にＰが進む距離ｔ3の６倍。また、t=t3〜35・2/3にQが動く距離もｔ3である。
　よって、ｔ3×（６＋１）＝４×３５、ｔ3＝３５×４/７＝２０秒後。

（４）t４
　t=0〜t4間でQが進む距離は、同じ時間にＰが進む距離ｔ4の６倍。また、t=35・2/3〜ｔ4にQが動く距離もｔ4である。
　よって、ｔ4×（６−１）＝４×３５、ｔ4＝３５×４/５＝２８秒後。

（５）t５
　Ｑの動く速さはＰの６倍であることから、t=0〜t5間でQが進む距離は、同じ時間にＰが進む距離ｔ5の６倍。また、t=t5〜35にQが動く距離もｔ5である。
　よって、ｔ5×（６＋１）＝６×３５、ｔ5＝３５×６/７＝３０秒後。

答：10、14、20、28、30秒後

（参考）

参考図4

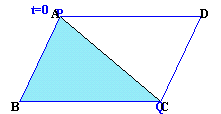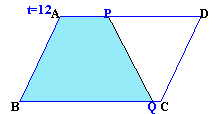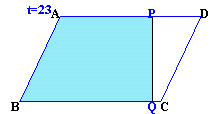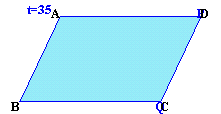
以上

３．解答例２（航介さん他）

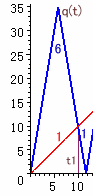
（１）t1、ｔ3、ｔ5
　　ｑ（ｔ）＝６×(３５×ｎ/６−ｔ）＋３５、ｐ（ｔ）＝ｔ（ただし、n=1、3、5）
　よって、
　　６×(３５×ｎ/６−ｔ）＋３５＝ｔ、７ｔ＝（ｎ＋１）×３５、ｔ＝（ｎ＋１）×５
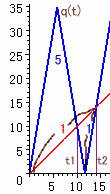
　すなわち、t1=10、t3=20、t5=30

（２）t2、ｔ4
　　ｑ（ｔ）＝６×(ｔ−３５×ｎ/６）、ｐ（ｔ）＝ｔ（ただし、n=2、4）
　よって、
　　６×(ｔ−３５×ｎ/６）＝ｔ、5ｔ＝ｎ×３５、ｔ＝ｎ×7
　すなわち、t2=14、t4=28

以上