第１１８問の解答

１．問題　［時計算］

図１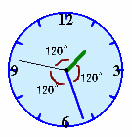
問題図		 図２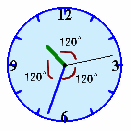
参考図1

　時計の時針・分針・秒針の３本の針が左図のように３６０度を３等分するような位置関係になることが、１日に何回あるでしょうか？

　

２．解答例１

午前と午後は、全く同じなので半日の１２時間を考えればよい。

また、３本の針が図１のような位置関係にあるものの時刻をｈとすると、（１２−ｈ）は、ちょうど左右対称に折り返したものとなるので、図２の位置関係のものになる。

従って、図１、図２のタイプのものは個数が同じなので、図１のタイプのもののみを考えることとする。

０時から時刻ｔ（ｈ時ｍ分ｓ秒）まで時針・分針・秒針が回転する角度をｘ、ｙ、ｚとする。（０≦ｈ＜１２）
ただし、１時間分（３０度）を単位として、小数部も含めて考えることとする。

参考図2

ｘ＝ｈ、ｙ＝１２ｈ、ｚ＝７２０ｈ　となります。

まず、時針と分針の角度が１２０度となる場合を考えます。
最初に１２０度の間隔になるのは、ｙ−ｘ＝１１ｈ＝１２ｎ＋４、従ってｈ＝（１２ｎ＋４）/１１のときになります。ただし、０≦ｈ＜１２より、ｎ＝０、１、・・・、１０の１１回あります。

ｍ、ｓは、６０ｈ、６０×６０ｈをそれぞれ１２で割った余りとして求められます。

参考図3

参考図4

参考図5

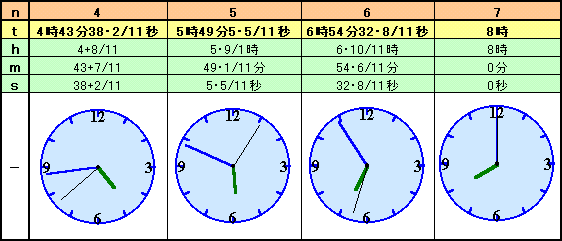
従って、分針と秒針の角度が１２０度、すなわちｓ−ｍ＝２０となるときは、この１１回のうち１度もないことが分かります。

答：０回

（参考）
ｙ＝１２ｈ＝１２/１１×（１２ｎ＋４）、ｚ＝６０ｙより、
ｚ−ｙ＝５９ｙ＝５９×１２/１１×（１２ｎ＋４）を１２で割ったあまりが４となるには、
１２ｎ＋４が１１の倍数となることが必要。
ところが、このときｙもｚも１２の倍数となるので、分針・秒針とも０時の位置にある。
実際、１２ｎ＋４が１１の倍数となるのは、ｎ＝７のときでちょうど８時のときである。

以上