第121問の解答
1.問題 [平面図形]
|
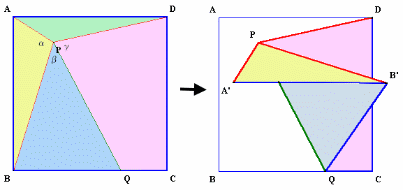
左図のように、正方形の折り紙を、 α=105°、β=45°とすると、γは何度になるでしょう? |
2.解答例1
(Taroさん、Mikiさん、ありっちさん、DrKさん、数楽者さん、あんみつさん、有無相生さん、他多数)
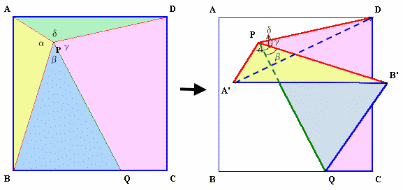
右図で、角A'PD=角A'PB'+角QPD−角QPB'が成り立ちます。
すなわち、δ=α+γ−β、よってα+γ=β+δ。ところが、(α+γ)+(β+δ)=360°より、
α+γ=β+δ=180°、
γ=180°−β=180°−105°=75°となります。答:75°
以上
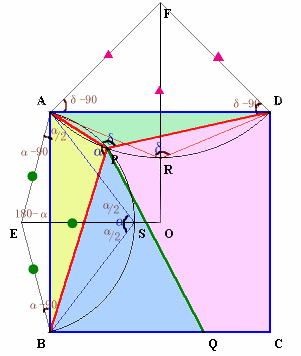
(参考)点P、Qを求める。
α、δが一定値(α、δ>180°)をとるとき、点P、Qは円弧AB、AD上を動くので、これらの2つある交点のうち、点Aでないほうとなる。(図1)
従って、点Pは1個のみ存在する。
図1
図2
円弧ABの中心Eは、正方形の中心Oと辺ABの中点を延長した線上にある。
円弧ABとOEの交点をSとする。AS=BSより、角ASE=角ASB/2=α/2。
EA=ESより、角EAS=角ESA=α/2。よって、角AES=180°−(角EAS+角ESA)=180°−α。
角EAB=角EBA
=180°−(角AES+90°)
=180°−(180°−α+90°)
=α−90°。従って、円弧ABの中心Eは、A、Bよりα−90°の角度で直線をそれぞれ引いたときの交点となる。
同様にして、円弧ADの中心Fは、A、Dよりδ−90°の角度で直線をそれぞれ引いたときの交点となる。
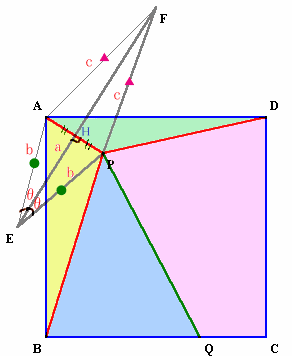
さて、点Pは、円Eの円周上、円Fの円周上にあるので、EFとAPの交点をHとすると、
EFとAPは直交し、AH=HPとなる。従って、点Pは、点Aから辺EFに垂線を下ろし、その足をHとして、HP=AHとなるように点Pを求めればよいことになる。
また、点Qは、点Pから角DPQ=γとなるよう直線を引き、辺BCとの交点とすれば良い。
以上