第１２２問の解答

---

１．問題　［速度］

Ａ地点からＢ地点まで、新幹線と高速バスを同じ距離だけ乗った場合と、 Ｂ地点からＡ地点まで、新幹線と高速バスを同じ時間だけ利用したときでは、 所用時間は１８分の差がありました。 新幹線は時速２１０ｋｍ、高速バスは時速１２０ｋｍの一定速度で走るものとすると、 Ａ地点からＢ地点までは何ｋｍ離れていることになるでしょう。

---

２．解答例１(中村明海さん、萬田銀次郎(ミナミの鬼)さん、ありっちさん、他多数)

Ｂ地点からＡ地点までの平均時速、所用時間をv1km、t1時間、
Ａ地点からＢ地点までの平均時速、所用時間をv2km、t2時間、および
Ａ地点からＢ地点までの距離をｄkmとします。

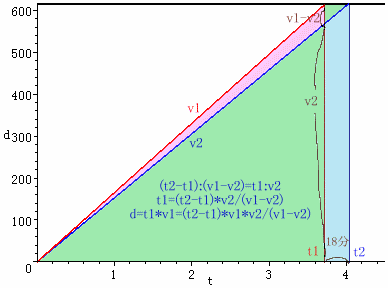
上図で緑色の三角形が相似なことからより、
　　（ｔ２−ｔ１）：（ｖ１−ｖ２）＝ｔ１：ｖ２、
　　（ｔ２−ｔ１）×ｖ２＝ｔ１×（ｖ１−ｖ２）、
　　ｔ１＝（ｔ２−ｔ１）×ｖ２／（ｖ１−ｖ２）　となります。

　　ｖ１＝（２１０＋１２０）／２＝１６５km/h、　　　　　　　　・・・算術平均
　　ｖ２＝２／（１/２１０＋１/１２０）＝１６８０/１１km/h　・・・調和平均

よって、
　　ｖ１−ｖ２＝１６５−１６８０/１１＝１３５/１１km/h

また、ｔ２−ｔ１＝１８/６０＝３/１０hであるから、
　　ｔ１＝（３/１０）×（１６８０/１１）／（１３５/１１）＝５６/１５時間、
　　ｄ＝ｔ１×ｖ１＝５６/１５×１６５＝６１６km　となります。

あるいは、
　210×t1/2+120×t1/2 = d 
　(d/2)/210 +(d/2) /120 = t1+0.3 
を解いて、ｔ１＝５６/１５時間、ｄ＝６１６kmを得る。

答：６１６ｋｍ

以上

---

２．解答例１(Taroさん、 萬田銀次郎(ミナミの鬼)さん、わかさひ君他多数)

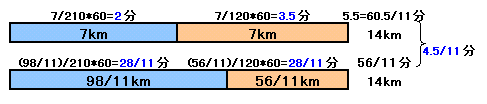
仮にｄ＝１４kmとしてみる。

ＡからＢまでは、それぞれ７kmを２１０km/h、１２０km/hで走るので、
所要時間は、７/２１０×６０＝２分、および７/１２０×６０＝３．５分、
合計５．５＝６０．５/１１分となります。

ＢからＡまでは、新幹線と高速バスは走る時間は同じなので、
走行距離は２１０：１２０＝７：４。

よって、
　新幹線：　１４km×７/１１＝９８/１１km、
　高速バス：１４km×４/１１＝５６/１１km
を走ることになります。

所要時間は、
　新幹線：（９８/１１）／２１０×６０＝２８/１１分、
　高速バス：（５６/１１）／１２０×６０＝２８/１１分
合計５６/１１分走ることになります。

よって、所用時間の差は、６０．５/１１−５６/１１＝４．５/１１分になります。

ところが、実際の差は１８分だったので、１４kmの１８／（４．５/１１）＝４４倍、
すなわち、ｄ＝１４×４４＝６１６km　となります。

以上

---

（参考）平均について

ｘ、ｙを正の数とする。 　算術平均　：　（x+y）/2 　調和平均　：　1/((1/x+1/y)/2)=2xy/(x+y) 　幾何平均　：　√xy に関して、 調和平均≦幾何平均≦算術平均（等号はｘ＝ｙのとき）

例えば、ｘ＝２１０、ｙ＝１２０とすると、
　算術平均　：　（２１０＋１２０）／２＝１６５
　幾何平均　：　√（２１０×１２０）＝６０√７≒１５８．７５
　調和平均　：　２×２１０×１２０／（２１０＋１２０）＝１６８０/１１≒１５２．７３
と確かに成り立つ。

実際、
　　　算術平均−幾何平均＝(x+y)/2-√(xy)＝(√x-√y)²/2≧０
　　　幾何平均−調和平均＝√(xy)−2xy/(x+y)＝√(xy)・(√x-√y)²/(x+y)≧０
から証明できる。

以上

---