第１２４問の解答

---

１．問題　［平面図形］

左図の△ＡＢＣは、次のような三角形です。 面積を求めて下さい。 Ｄ、Ｅ、Ｆは、辺ＢＣ、ＣＡ、ＡＢの中点 ＦＰ、ＥＱはＡＤに垂直で長さはともに１５cm　 ＡＰ＝２０cm、ＰＱ＝１６cm、ＱＤ＝２０cm

---

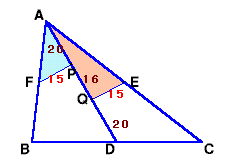２．解答例１(わかさひ君、清川育男さん、巷の夢さん、DrKさん、大岡敏幸さん、ハラギャーテイさん、他多数)

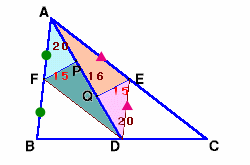
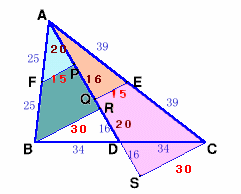
Ｂ、ＣからＡＤへ下ろした垂線の足をＲ、Ｓとします。

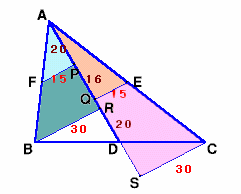
△ＡＢＲについて、中点連結定理より、ＢＲ＝２×ＦＰ＝３０cm。
同様に、ＳＣ＝２×ＱＥ＝３０cm。

△ＡＢＣ＝△ＡＢＤ＋△ＡＤＣ
　　＝１/２×ＡＤ×ＢＲ＋１/２×ＡＤ×ＱＥ
　　＝１/２×５６×３０×２
　　＝１６８０ｃｍ²。

答：１６８０ｃｍ²

以上

---

３．解答例２(航介さん他)

△ＡＦＤ＝１/２×ＡＤ×ＦＰ＝１/２×５６×１５＝４２０cm。
△ＡＥＤ＝１/２×ＡＤ×ＱＥ＝１/２×５６×１５＝４２０cm。

△ＡＢＣ＝△ＡＢＤ＋△ＡＤＣ
　　＝△ＡＦＤ×２＋△ＡＥＤ×２
　　＝４２０×２×２
　　＝１６８０ｃｍ²。

---

４．解答例３(きょえぴさん、ありっちさん、Taroさん他)

△ＡＦＰに三平方の定理を用いて、
　ＡＦ²＝ＡＰ²＋ＰＦ²＝２０²＋１５²＝６２５、
よって、ＡＦ＝２５cm、ＡＢ＝５０cm。 

△ＡＥＱに三平方の定理を用いて、
　ＡＥ²＝ＡＱ²＋ＱＥ²＝３６²＋１５²＝１５２１、
よって、ＡＥ＝３９ｃｍ、ＡＣ＝７８cm。

△ＡＢＣに中線定理を用いて、
　ＡＢ²＋ＡＣ²＝２（ＡＤ²＋ＢＤ²）
ＢＤ²＝（ＡＢ²＋ＡＣ²）／２−ＡＤ²
　　＝（５０²＋７８²）／２−５６²
　　＝１１５６
よって、ＢＤ＝３４cm、ＢＣ＝６８cm。 （注）

△ＡＢＣは、ヘロンの公式を用いると、三辺が５０cm、７８cm、６８cmだから、 ｓ＝（５０＋７８＋６８）／２＝９８として、
△ＡＢＣ＝√９８（９８−５０）（９８−７８）（９８−６８）
　　＝√２８２２４００
　　＝１６８０cm²。

（注）ＢＤ＝ＤＣを求める別の方法：
　ＲＤ＝ＡＤ−ＡＲ＝５６−４０＝１６
　△ＢＤＲに三平方の定理を用いて、
　ＢＤ²＝ＢＲ²＋ＲＤ²＝３０²＋１６²＝１１５６
　よって、ＢＤ＝３４cm。

（参考）ＱＤ＝ＡＰに等しいので長さが与えられていなくても良い 　　また、ＢＤ＝ＤＣも題意より求まるので条件に無くて良い。 △ＢＤＲと△ＣＤＳは、相似でＢＲ＝ＣＳ＝３０cmなので合同。 よって、ＲＤ＝ＤＳ、ＢＤ＝ＤＣ。 従って、 ＡＤ＝（ＡＲ＋ＡＳ）／２ 　　＝（ＡＰ×２＋ＡＱ×２）／２ 　　＝ＡＰ＋（ＡＰ＋ＰＱ） ＡＤ＝ＡＰ＋ＰＱ＋ＱＤでもあるので、ＡＰ＝ＱＤとなる。

---

５．解答例４(トトロ＠Ｎさん他)　

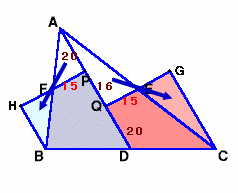
図１

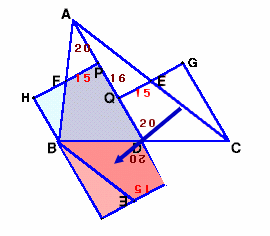
図２

△ＡＦＰを１８０度回転しＦＢに、△ＡＥＱを１８０度回転しＥＣに合わせる。（図１）
さらに、四角形ＱＧＣＤを１８０度回転しＢＤに合わせる。（図２）

出来た図形は、辺の長さが２×ＦＰ＝３０cm、ＡＱ＋ＱＤ＝５６cmの長方形となる。

よって、△ＡＢＣ＝長方形の面積＝３０×５６＝１６８０cm²となる。

---