第125問の解答
1.問題 [整数の性質]
|
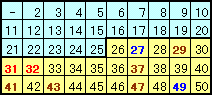
ある大きな整数Xがあります。この整数Xを2から50までの全ての整数で割ってみたところ、Xを割ったときの答が整数にならないものが、AとBの2個だけでした。また、AとBの差は1でした。 では、この整数A、Bは何と何でしょうか? |
2.解答例1(Taroさん、わかさひ君、長野美光さん、АЯСさん、ともき先生、清川育男さん、あずさ猫さん、micky99558さん、他多数)
整数NがA、Bに該当する可能性について考えましょう。
1.Nの素因数が複数のとき
N=P×Qとします。(ただし、2≦N≦50で、P、Qは互いに素な整数)
NとP、Qの差は1より大なので、題意よりXをNで割り切れ、P、Qでは割り切れないことになるが、これはありえない。よって、Nは、素因数が1個でなければならない。 ・・(1)
2.Nの倍数が50以下に存在するとき
M=N×Pとします。(だだし、2≦N、M≦50、Pは2以上の整数)
NとPの差は1より大なので、題意よりXをNで割り切れ、Mでは割り切れないことになるが、これはありえない。従って、2≦N≦25ならば、2<M=2N≦50となり、50以下の倍数が存在するので不適。
よって、25≦Nでなければならない。 ・・(2)3.素数のべき乗(素数自身を含む)のとき
1.素因数が1個の場合に該当するが、(2)よりNの倍数が50以下に存在してはいけないので、ある素数のべき乗のなかでは、50以下の最大値のみが該当する可能性がある。
もし、その素数が奇数とするとべき乗であるNも奇数となり、N−1、N+1とも偶数になるので、N−1、N+1のいずれかが2のべき乗でなければならない。
また、連続した整数のうちいずれかは偶数なので、A,Bともに素数とはならない。
以上から、A、Bのいずれかは、2のべき乗で最大のもの、すなわち25=32であることが分かる。
32−1=31は素数、32+1=33=3×11なので31が適。
答:31、32以上