第１２６問の解答

１．問題　［立体図形・平面図形］

左図は、１辺が４ｃｍで頂角が４５度の二等辺三角形４個と、正方形１個を使って作られた正四角錐です。

この立体の表面積は何ｃｍ²になるでしょうか？

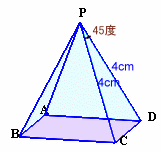２．解答例１(やすさん、マツダさん、長野美光さん、Taroさん、他多数)

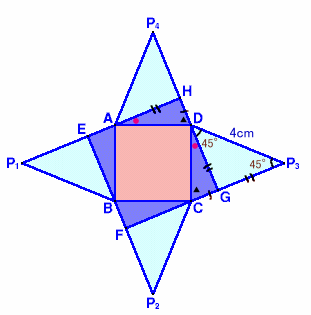
展開図は図１のように、正方形ＡＢＣＤの各辺に、二等辺三角形AP₁B、BP₂C、CP₃D、DP₄Aを合わせた図形となります。

図１
図２

BからAP₁に下ろした垂線の足をE、CからBP₂に下ろした垂線の足をF、・・、G、Hとします。

三角形DGP₃について、∠DP₃C＝４５度、∠DGP₃＝９０度より、∠P₃DG＝４５度、よって三角形DGP₃は、対角線が４ｃｍの直角二等辺三角形となります。
従って、BEP₁、CFP₂、DGP₃、AHP₄を合わせると、図２のとおり一辺が４ｃｍの正方形となります。

また、三角形DCGと三角ADHは合同だから、HD＋DG＝P₃＋CG＝４ｃｍで、∠HDA+∠CDG＋∠ADC＝∠HDA+∠DCG＋９０度＝１８０度だから、
HDGは一直線上にある。

よって、ＥＦＧＨは、一辺が４ｃｍの正方形となる。

以上から、求める面積＝４×４＋４×４＝３２ｃｍ²となります。

答：３２cm²

以上

３．解答例２(数楽者さん他)

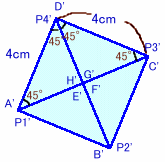
展開図を２枚用意し、１つは四角形P₃DOCと同じ図形を４個、１つは正方形ABCDと二等辺三角形P₃BAと同じ図形を４個に分割して、これらを図４のように合わせます。

図３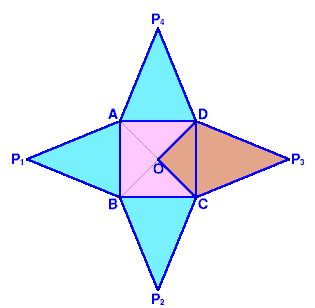

図４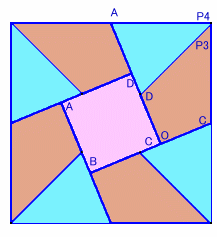

図４が一辺８ｃｍの正方形とぴったり当てはまることは容易に示されるので、求める面積は、８×８／２＝３２ｃｍ²となる。

４．解答例３(トトロ＠Ｎさん、あんみつさん、kakeruさん他)

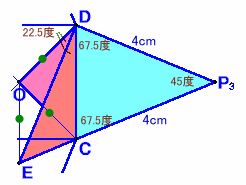
解答例２の四角形P₃DOCを等積変形します。
Ｏから辺DCに平行に引いた直線と辺P₃Cの延長線との交点をＥとします。

三角形OECは、∠OEC＝∠DCP₃＝６７．５度、∠EOC=４５度だから、三角形P₃DCと相似な二等辺三角形となる。
よって、OE＝OC。

従って、ＯＤ＝ＯＣ＝ＯＥとなり、三角形OEDは二等辺三角形となる。
よって、∠ODE＝（１８０－（４５＋９０））／２＝２２．５度。
∠EDC=４５度－２２．５度＝２２．５度、∠EDP₃＝６７．５＋２２．５＝９０度。

従って、三角形EDP₃は、１辺が４ｃｍの直角二等辺三角形となる。
面積は、１/２×４×４＝８ｃｍ²。

求める展開図の面積は、この４倍＝３２ｃｍ²となる。

５．解答例４(Taroさん、たなかさん、杉本未来さん、大岡敏幸さん、Ｎａｇａｈｉｒｏさん、しゅうさん、井合宗太郎さん、ハラギャーテイさん、有無相生さん、DrKさん、みのちゃん、っはらさん他)

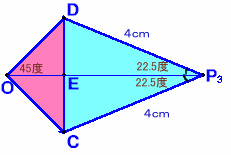
DP₃＝ａ＝４ｃｍ、∠DP₃E＝θ＝２２．５度とします。

DE＝a・ｓｉｎθ、EP₃＝ａ・ｃｏｓθ、
よって、
△P₃DC＝ＤＥ×EP₃＝ａ²×ｓｉｎθ・ｃｏｓθ＝１/２×ａ²×ｓｉｎ２θ。
△OCD＝OE・DE＝ａ²・ｓｉｎ²θ＝１/２×ａ²×(1-ｃｏｓ2θ)
　＝１/２×ａ²×(1-sin２θ)。　（２θ＝４５度だから）

四角形ODP₃C＝△P₃DC＋△OCD＝１/２×ａ²＝８ｃｍ²。
よって、求める展開図の面積＝四角形ODP₃C×４＝３２ｃｍ²。