図1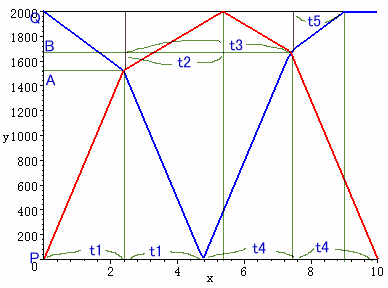 |
図2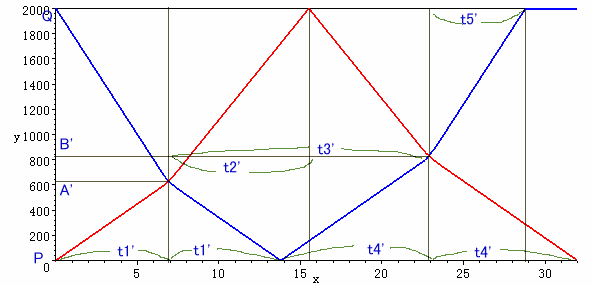 |
第127問の解答
1.問題 [旅人算]
ゆたか君は、買ったばかりのバイクを持っています。友達のA君も新品の自転車を買ったと聞いて、A君をP、Q2地点を結ぶ片道(ア)mのツーリングコースに誘いました。
ゆたか君は、この自転車で毎分160m、A君は毎分200mで走ることができ、バイクは誰が運転しても毎分640mの一定速度で走ります。さて、バイクの試乗を兼ねて次のような計画を立てました。
ゆたか君は最初バイクに乗ってP地点を出発し、同時刻にA君は自転車に乗ってQ地点を出発します。2人が出会うと、その場で乗り物を交換し、ゆたか君はQ地点まで進んで折り返し、A君はP地点まで進んで折り返します。再び出会ったところで、もう一度乗り物を交換して、元の地点まで戻る予定でした。
ところが、出発直前になってゆたか君は、バイクにガソリンを入れるのを忘れたことに気づいたので、仕方なくバイクの替わりに歩くことにしました。歩く速度は、2人とも毎分90mです。
この結果、当初1分遅れでゆたか君はゴールする予定だったのですが、実際には(イ)分(ウ)秒遅れてしまいました。文中の(ア)、(イ)、(ウ)の数値を答えて下さい。
2.解答例1(sambaGREENさん、中村明海さん、有無相生さん、他多数)
最初の計画でゆたか君とA君が出会う地点をA、B(図1)、実際に出会った地点をA'、B'(図2)とします。また、それぞれの区間の所要時間を図のようにとります。
図1 |
図2 |
[計画]
ゆたか君は、AQ+QB間をt3分で走っており、同じ時間にA君がバイクで走る距離と合わせるとPQ間(dmとする)を往復することとなるので、
2d=(640+160)×t3、QA+QB=160×t3
よって、QA+QB=2d×160/(640+160)=d×2/5。ゆたか君、A君ともPA、PB間をバイクで走る時間は同一なので、所用時間の差はQA+QB間を自転車で走る時間の差に等しい。
よって、d×2/5×(1/160−1/200)=1、
d=5/2×160×200/(200−160)
=2000m[実際]
計画と同様にして、QA'+QB'=2d×160/(90+160)=d×32/25。所用時間差は、
d×32/25×(1/160−1/200)
=32/25/2/5
=16/5分
=3分12秒
となります。
答:(ア)2000m、(イ)3分(ウ)12秒
以上