第１２８問の解答

---

１．問題　［平面図形］

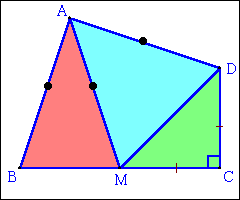
四角形ＡＢＣＤの辺ＢCの中点をＭとして、左図のように３つの部分に区切ったところ、△ＡＢＭと△ＡＤＭは二等辺三角形に、△ＤＣＭは直角二等辺三角形になりました。 　このとき、△ＡＢＭ：△ＡＤＭ：△ＤＣＭの面積比を答えて下さい。

---

２．解答例１(ありっちさん、小太りおじさん、他)

ＡからＢＣに下ろした垂線の足をＥ、ＡＣとＭＤとの交点をＦ、ＦからＢＣに下ろした垂線の足をＧとします。

△ＡＢＭは二等辺三角形だから、ＥはＢＭの中点となり、ＢＥ＝ＥＭ。
△ＡＤＭ、△ＤＣＭはともに二等辺三角形だから、ＦはＭＤの中点となり、ＭＦ＝ＦＤ。
よって、中点連結定理より、ＭＧ＝ＧＣ。
ＢＭ＝ＭＣなので結局、ＢＥ＝ＥＭ＝ＭＧ＝ＧＣ。

ＭＦ＝ＦＤなので、△ＭＦＣ、△ＣＦＤとも直角二等辺三角形となり、
∠ＡＣＢ＝４５度、よって△ＡＣＥも直角二等辺三角形。

△ＡＥＣと△ＦＧＣは相似、相似比はＥＣ：ＧＣ＝３：１。
よって、ＡＥ：ＦＧ＝３：１、ＡＦ：ＦＣ＝ＥＧ：ＧＣ＝２：１。

△ＡＢＭと△ＦＭＣは、底辺の長さが等しい（ＢＭ＝ＭＣ）ので、面積比は高さの比＝ＡＥ：ＦＧ＝３：１。
△ＤＣＭ＝２×△ＦＭＣなので、△ＡＢＭ：△ＤＣＭ＝３：２。

△ＡＤＭと△ＤＣＭは、底辺の長さ（ＤＭ）が等しいので、面積比は高さの比＝ＡＦ：ＦＣ＝２：１＝４：２。

よって、△ＡＢＭ：△ＡＤＭ：△ＤＣＭ＝３：４：２となります。

　

答：３：４：２

以上

---

３．解答例２(Taroさん、わかさひ君、 うっしー&翔太さん、他多数)

ＢＭの中点をＥとし、二等辺三角形ＡＢＭの半分ＡＢＥを移動し、ＡＢをＡＤと重ねたものをＡＤＨとします。

∠ＡＤＨ＝∠ＡＢＥ＝∠ＡＭＥ、∠ＡＤＭ＝∠ＡＭＤ、∠ＭＤＣ＝∠ＤＭＣ。
∠ＡＤＨ＋∠ＡＤＭ＋∠ＭＤＣ＝∠ＡＭＥ＋∠ＡＭＤ＋∠ＤＭＣ＝１８０度。
よって、Ｈ、Ｄ、Ｃは一直線上に並ぶことになり、四角形ＡＥＣＨは正方形となります。

ＢＥ＝ＥＭ＝１とおくと、ＭＣ＝ＢＭ＝２、よってＥＣ＝３となります。
よって、正方形ＡＥＣＨ＝３×３＝９。

さて、△ＡＢＭ＝１/２×２×３＝３、△ＡＥＭ＝△ＡＤＨ＝３/２。
△ＤＣＭ＝１/２×２×２＝２。

よって、△ＡＤＭ
　　＝正方形ＡＥＣＨ−（△ＡＥＭ＋△ＡＤＨ＋△ＤＣＭ）
　　＝９−（３/２＋３/２＋２）
　　＝４。

よって、△ＡＢＭ：△ＡＤＭ：△ＤＣＭ＝３：４：２。

---

４．解答例３(大岡敏幸さん、あまれっとさん、他)

ＡＤを結び、中点をＰとし、ＡＣとＤＭの交点をＱとします。

ＢＭ＝ＭＣ＝２とすると、ＣＤ＝ＭＣ＝２。
ＢＤ²＝ＢＣ²＋ＣＤ²＝４²＋２²＝２０。
よって、ＢＤ＝２√５、ＢＰ＝√５。

　　∠ＢＡＭ＋∠ＭＡＤ
　＝（１８０度−２×∠ＡＭＢ）＋（１８０度−２×∠ＡＭＤ）
　＝２×（１８０度−∠ＡＭＢ−∠ＡＭＤ）
　＝２×４５度
　＝９０度
よって、△ＡＢＤは直角二等辺三角形。
△ＡＢＤ＝２×△ＡＢＰ＝５。

従って、
　　　四角形ＡＢＣＤ
　＝△ＡＢＤ＋△ＤＢＣ
　＝５＋４＝９。

よって、△ＡＢＭ＝△ＡＭＣ＝△ＡＣＤ＝３。

また、△ＤＣＭ＝２だから
　　△ＡＤＭ
　＝四角形ＡＢＣＤ−△ＡＢＭ−△ＤＣＭ
　＝９−３−２
　＝４。

よって、△ＡＢＭ：△ＡＤＭ：△ＤＣＭ＝３：４：２。

---

５．解答例４(中村明海さん、杉本未来さん、巷の夢さん、他)

ＢＭの中点をＥとし、ＤＭの中点をＦとします。

ＡＥ＝ｈとすると、
ＡＭ²＝ＡＥ²＋ＥＭ²＝ｈ²＋１²
ＡＤ²＝ＥＣ²＋（ＡＥ−ＣＤ）²＝３²＋（ｈ−２）²。
ＡＭ＝ＡＤだから、
　ｈ²＋１²＝３²＋（ｈ−２）²
　４ｈ＝１２
となり、ｈ＝３を得る。
よって、ＡＭ²＝３²＋１²＝１０。

ＭＦ＝ＦＤ＝√２より、ＡＦ²＝AM²−ＭＦ²＝１０−２＝８。
従って、ＡＦ＝２√２。

よって、△ＡＢＭ＝３、△ＡＤＭ＝√２×２√２＝４、△ＤＣＭ＝２。
△ＡＢＭ：△ＡＤＭ：△ＤＣＭ＝３：４：２。

---