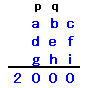第１２９問の解答

---

１．問題　［虫食い算、組み合わせ］

０から９までの数字を使って３桁の整数を３個つくり、これを大きい順に並べます。 このとき、１つの数字は、１回しか使わないようにします。 ３つの整数の和がちょうど２０００になるような３数の組み合わせは何通りあるでしょうか？

---

２．解答例１(Taroさん、たなかさん、香川仁志さん、C-Dさん、ZERO/織田病院さん、中村明海さん、中学への算数にチャレンジさん、sekkiさん、他多数)

３つの整数をabc、def、ghi（ただし、abc>def>ghi）とします。
また、百位、十位への繰り上がりをｐ、ｑとします。
a、d、gは異なるので、a>d>gとなる。

　　p＋a＋d＋g＝２０　　　　・・・　（１）
　　q＋b＋e＋h＝p×１０　・・・　（２）
　　　　ｃ＋ｆ＋ｉ＝q×１０　　・・・　（３）

辺々加えて、
　　p＋q＋（a＋b＋ｃ＋d＋ｅ＋ｆ＋g＋ｈ＋ｉ）＝（p＋q）×１０＋２０
ここで、ｓ＝a＋b＋ｃ＋d＋ｅ＋ｆ＋g＋ｈ＋ｉとおくと、
　　ｓ＝（p＋q）×９＋２０

ｓは、０、１、２、・・・、９から選んだ９つの整数の和だから、
　　０＋１＋２＋・・・＋８＝３６≦ｓ≦１＋２＋３＋・・・＋９＝４５
よって、１６≦（p＋q）×９≦２５、p＋q＝２となる。

繰り上がりがないと和の各桁が０にはならないので、p、q≧１。
よって、p＝q＝１となる。

（１）、（２）、（３）より、
　　　　a＋d＋g＝１９　・・・　（４）
　　　　b＋e＋h＝９　　・・・　（５）
　　　　ｃ＋ｆ＋ｉ＝１０　　・・・　（６）

よって、ｓ＝１９＋９＋１０＝３８となり、１０個の数字のうち、残る数字は４５−１８＝７である。

（４）、（５）、（６）を満たす（a、d、g）、（b、e、h）、（c、f、i）が１組あったとき、
３つの整数を選ぶ組み合わせは、
　b、e、hの並び替え₃C₂＝６通り×ｃ、ｆ、ｉの並び替え₃C₂＝６通り
の３６通りとなる。

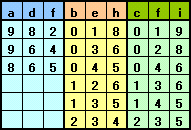
さて、（４）、（５）、（６）をそれぞれ満たす整数の組み合わせは表１、
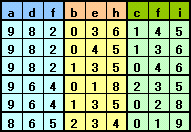
また、（４）、（５）、（６）を全て同時に満たす組み合わせは表２の６通りである。

表１

表２

　よって、求める場合の数は、３６×６＝２１６通りとなる。

答：２１６通り

以上

---