第130問の解答
1.問題 [船の速さ]
|
一定の速さで流れている河の上流と下流を、2隻の同性能の船を使って毎日往復している定期便があります。 |
2.解答例1(ありっちさん、C-Dさん、Taroさん、 長野美光さん、まさぴょんさん、他)
静水上の船の速さ、川の流れる速さをV、V’、下り便の速さ、上り便の速さをv1、v2とします。ダイアグラムを書くと下図のようになります。
第130問の解答
1.問題 [船の速さ]
一定の速さで流れている河の上流と下流を、2隻の同性能の船を使って毎日往復している定期便があります。
ある日、この2隻のうち上り便の出発時刻が13分遅くなってしまいました。そのため、本来11時11分にすれ違う予定だったところが、実際に2隻がすれ違ったのは11時16分だったそうです。
では、ここで使用している船は、静水上では川の流れの何倍の速さで走ることが出来るでしょう?
2.解答例1(ありっちさん、C-Dさん、Taroさん、 長野美光さん、まさぴょんさん、他)
静水上の船の速さ、川の流れる速さをV、V’、下り便の速さ、上り便の速さをv1、v2とします。ダイアグラムを書くと下図のようになります。
t1+5=13+t2より、t2−t1=13−5=8分。
上り便が13分遅れた間に下り便はv1×13だけ走り、これは(v1+v2)×(t2−t1)=(v1+v2)×8と等しいことから、
(v1+v2)×8=v1×13
よって、
(v1+v2):v1=13:8。
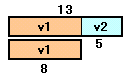
v1=V+V’、v2=V−V’だから、V:V’=(8+5):(8−5)=13:3になります。
答:13/3以上