第44問の補題
正数X1、X2、・・、Xnは、和がZで一定の時、Y=X1×X2×・・×Xnは、X1=X2=・・=Xn=Z/nのとき最大となる。 相加相乗平均の関係より、(X1+X2+・・+Xn)/n≧(X1×X2×・・×Xn)1/n
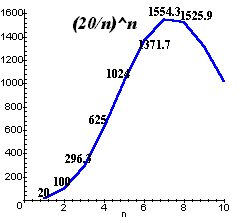
よって、X1×X2×・・×Xn≦(Z/n)n(等号は、X1=・・が全て等しいとき)(参考)n=1,2,・・のときの(20/n)nのグラフ
以上
第44問の補題
正数X1、X2、・・、Xnは、和がZで一定の時、Y=X1×X2×・・×Xnは、X1=X2=・・=Xn=Z/nのとき最大となる。 相加相乗平均の関係より、(X1+X2+・・+Xn)/n≧(X1×X2×・・×Xn)1/n
よって、X1×X2×・・×Xn≦(Z/n)n(等号は、X1=・・が全て等しいとき)(参考)n=1,2,・・のときの(20/n)nのグラフ

以上