問題[平面図形]
|
|
|
|
|
|
|
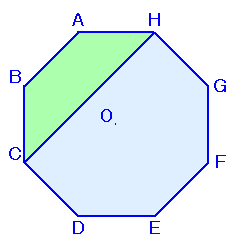 |
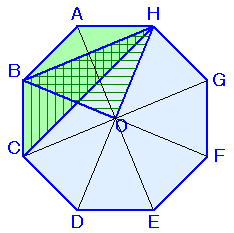
左図で、斜線部分の面積は全体のどれだけの割合ですか? |
|
|
|
|
|
|
解答例1[Oから補助線 、等高図形の利用]
| なにわさん、くりこめっちさん、HAJIさん、浜直君さん、ショウさん、 kasamaさん、智乃介さん、りかさん、相楽祥吾さん、ピーターラビットさん、 ともこさん、もありすさん、他 |
対称性からBHとCGが平行なことが分かります。
よって、△BCHと△BOHは底辺BHが共通で高さが等しいので合同。従って、
四角形ABCH
=△ABH+△BCH
=△ABH+△BOH
=△OHA+△OAB
=△OAB×2正八角形ABCDEFGH=△OAB×8だから、
四角形ABCH/正八角形ABCDEFGH=1/4
と求まります。答 1/4
以上
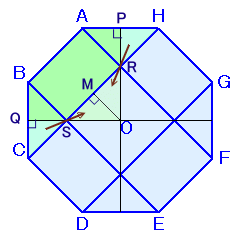
解答例2 [補助線、分割・合同、4枚重ね合わせ]
| 川村高雅さん、長野 美光さん、塾講師さん、 龍さん、吉田貴法さん、ともこさん、 tekiさん、 他 |
上図のように補助線を引き、AHの中点をP、BCの中点をQ、AFとCHの交点をR、BEとCHの交点をS、およびRとSの中点をMとします。
RS=AB=AH=BCと対称性より、△AHR、△BCS、△RSOは合同な直角二等辺三角形となります。
従って、
四角形ABCH=五角形PABQO
=正八角形×1/4
と分かります。
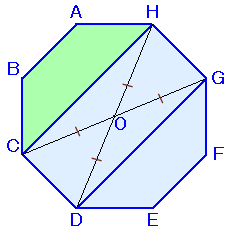
解答例3 [最も簡単な方法]
| 外科医長さん、他 |
OH=OC=OD=OGより、
△HCO=△OCD=△DOG=△GOHよって、
四角形(長方形)HCDG=△OCD×4=正八角形×1/2四角形ABCH=四角形EFGDより、
四角形ABCH=正八角形(1−1/2)×1/2=正八角形×1/4
と求まります。
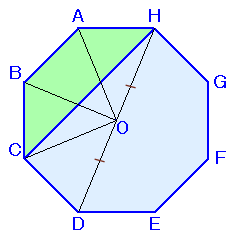
解答例4 [三角比]
| ゴンともさん、いさん、tomhさん、 kuri、他 |
OH=ODより、△OHC=△OCD。
よって、
四角形ABCH=五角形HABCO−△OHC
=△OHC×3−△OHC=△OHC×2以下同様。